本章讨论的目标规划均是指线性目标规划.首先让我们通过下面具体的引例，来了解目标规划的基本原理和基本概念.

例4－1　某工厂计划生产甲、乙两种产品，均需要经过A，B两道工序，有关信息如表4－1所示，问如何确定一周内的生产计划，使工厂获利最大？

表4－1

解　设x1，x2分别表示甲、乙两种产品在一周内的生产件数，则有线性规划模型如下：

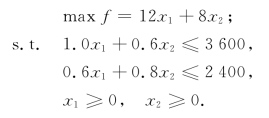
这个模型是在现有资源约束条件下，追求利润的最大化.但是，在现代企业管理决策中，决策者考虑的目标和因素往往是多方面的，不仅仅是唯一的目标利润最大化.

例如，决策者在现有资源约束的条件下，可以从这样一个角度来思考这个生产计划问题：首先确定一个合理的利润目标期望值，然后寻求优化的生产经营方案，以实现预期的利润目标.这里决策者追求的是实现既定利润目标期望值的优化决策方案，而不是简单、绝对的利润最大化.比如，该工厂决策者依据市场需求预测，综合考虑各方面因素，希望该周内实现利润值42 000元（称它为目标期望值），则问题转化为如何确定最优生产计划，实现42 000元的利润目标？由此产生的问题是这一目标期望值能否实现？如不能实现，超过的偏差或不足的偏差是多少？对此类问题，线性规划模型就有它的局限性.查恩斯（A.Charnes）和库柏（W.Coopre）于1961年创立的目标规划理论，通过引入偏差变量、目标约束等概念解决了这方面的问题.下面，我们结合本例对目标规划的基本概念逐一进行介绍.

负偏差变量d－——实现值未能达到目标期望值的偏差值，d－≥0；

正偏差变量d＋——实现值超过目标期望值的偏差值，d＋≥0.

对于例4－1，如果我们希望实现利润目标期望值42 000元，那么在引进偏差变量d－和d＋后，可以把这个要求用下式来表示：

我们将它放入约束条件中，并称之为目标约束.相应地，模型中原来的约束条件称为系统约束.显然，在规划实现某一目标期望值时，对于偏差变量d－和d＋，显然有d－·d＋＝0，即只可能出现下列3种情形之一：

①超额完成利润的目标期望值，d＋＞0，d－＝0；

②未能达到利润的目标期望值，d－＞0，d＋＝0；

③恰好完成利润的目标期望值，d－＝0，d＋＝0.

目标约束相对于系统约束来说是一种“软约束”.所谓“软约束”，是指目标约束中目标函数与目标期望值之间没有硬性的约束关系，目标期望值可能恰好满足，可能不满足，也可能过量满足.其具体满足的程度，可通过偏差变量d－和d＋的取值加以衡量.

对于函数f来说，根据决策者的期望，其实现的目标要求可以写成下面3种情形之一：(www.daowen.com)

①要求恰好达到目标期望值，表达成min f＝d－＋d＋.如果d－＋d＋＝0，就说明恰好实现目标期望值；

②希望超过目标期望值，即未达到目标期望值的偏差变量d－为最小，表达成min f＝d－.当d－＝0时，则完全实现该目标.

③希望不超过目标期望值，即超过目标期望值的偏差变量d＋为最小，表达成min f＝d＋.当d＋＝0时，则完全实现该目标.

为了区别于原来线性规划中目标函数的意义，上述函数f称为目标规划的达成函数.

如果例4－1中决策者希望实现超过42 000元的利润目标，引进偏差变量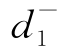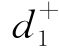，，则我们可以建立下列目标规划模型：

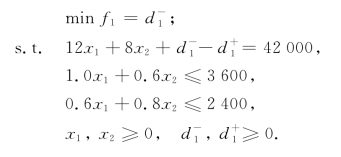
上述问题为单目标决策优化问题.在现实问题中，系统的目标常常是多元化的.比如例4－1，若工厂在制定最优生产计划时，决策者除了希望实现超过42 000元的利润目标外，根据市场和资源条件又提出如下两个目标：尽可能扩大甲产品的生产，使甲产品的数量不低于3 300件的目标期望值；尽可能减少乙产品的生产，使乙产品的数量不超过480件的目标期望值.问工厂如何确定一周内的最优生产计划？

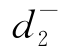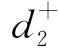类似于第一个目标的描述，对于甲产品的产量不低于3 300件的目标，引进偏差变量和，我们的要求可以如下体现：

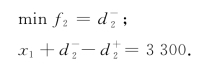
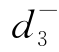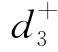对于乙产品的产量不超过480件的目标，引进偏差变量和，我们的要求可以如下体现：

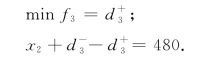
现在问题有了3个目标，那么这3个目标又怎样同时体现在一个目标规划模型的达成函数中呢？对于这类多目标决策问题，目标规划依据“系统目标分级、赋权，决策问题逐级优化求解”的基本原理，通过引进“目标优先因子”和“相对权重系数”等概念与参数，很好地解决了模型的描述和求解.

比如上述问题的3个目标，决策者根据目标的相对重要程度，定性地将它们分成两个层次的优先等级来加以考虑：利润超过42 000元的目标作为第一级目标；希望甲产品的生产数量不低于3 300件的目标，与乙产品的生产数量不超过480件的目标同时属于第二级，但是前者比后者在同一级中又相对重要一些.为了表达上述目标分级要求，我们引入2个目标优先因子P1和P2：P1≫P2.符号“≫”表示一个定性的优先关系，表示第一级的目标远远重要于第二级的所有目标，它们属于不同层次的目标.另外，由于问题的第二级目标中有2个目标，为区别其相对重要程度，引进相对权重系数来体现这个要求（这里权重系数的第一个下标t表示所在的优先等级、第二个下标q表示偏差变量的排列顺序号）.于是，我们将上述问题的达成函数表示为f＝，相应的目标规划模型如下：

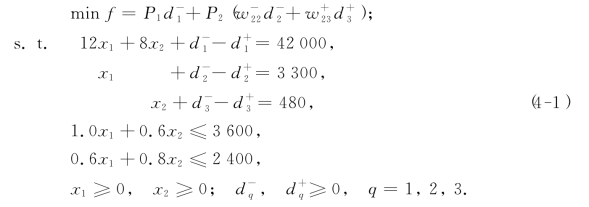
在实际问题中，我们往往给相对权重系数以具体的数字.例如对上面这个模型，可取

在求解上述问题时，目标规划按照逐级优化原则，首先考虑第一级目标——利润目标（超过42 000元）的实现；其次，在利润目标不退化的前提下，再考虑第二级目标——甲产品产量目标（不低于3 300件）和乙产品产量目标（不超过480件）的尽可能实现，依此类推；对于第二级中的2个目标，假设，则首先考虑甲产品产量目标（不低于3 300件）的实现，在其不退化的前提下，再考虑乙产品产量目标（不超过480件）的尽可能实现.

通常，目标规划问题中各个目标的优先等级（优先因子）和同级目标中各个目标的相对权重系数，决策者应该经过专家评审讨论来决定.另外，在目标分级时，一般不同等级的目标，其度量单位可以不同，但同一等级的目标，其度量单位应该相同，以便研究确定其相对权重系数.