由于在变量个数相等的情况下，表上作业法的计算比单纯形法简单得多，因此，在求解实际问题时，在条件许可的情况下，人们常常尽可能把某些线性规划问题转化为运输问题的数学模型（简称运输模型）.

所谓建立运输模型，就是要给出运输收发平衡单位运价表如表3－1.在该表中，要求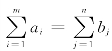，发点Ai至收点Bj都有单位运价cij（i＝1，…，m；j＝1，…，n）.下面我们来看几个具体的例子.

例3－8　（1）运输问题由表3－21给出，试建立运输模型.

（2）如果将表3－21中的b3改为14，又设B1、B2和B33个收点的需求量一旦不能满足时，就要承担缺货损失费.单位物资的缺货损失费分别为4，3和7.试建立运输模型.

解　（1）在表3－21中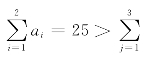，＝21，供大于需4个单位物资，供需不平衡.因此，我们要考虑将多余的4个单位物资在发点就地存储.现虚设一个收点B4，其需求量b4＝4，发点Ai至B4的单位运价ci4＝0，这样我们就得到了一个收发平衡的运输模型如表3－22所给.对表3－22求最优解.如果Ai至Bj的运量xi4＞0，则说明发点Ai就地存储物资xi4个单位.

表3－21

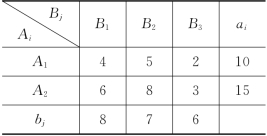
表3－22

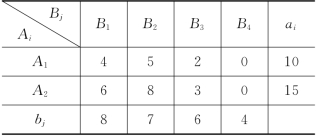
（2）现在b1＋b2＋b3＝8＋7＋14＝29，a1＋a2＝10＋15＝25，需大于供4个单位物资.虚设一个发点A3：a3＝4，A3至B1、B2和B3的单位运价就定为各收点Bj的单位物资缺货损失费4，3和7，得运输收发平衡单位运价表如表3－23.若表3－23的最优运输方案中运量x3j＞0，则说明Bj缺货x3j.

例3－9　（不平衡运输问题）　若发点Ai的发量ai必须运走，具体信息如表3－24所示，试建立运输模型.

表3－23

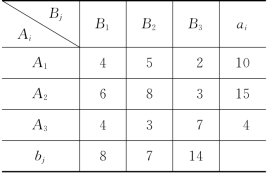
表3－24

解　现在＝45，而3个收点B1，B2，B3的最低需求量的和为30.由于发量45必须全部运走，为此虚设一个收点B4，b4＝15，Ai至B4的单位运价ci4确定如下：

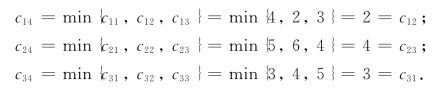
得运输收发平衡单位运价表如表3－25所示.

在求得运输模型表3－25的最优解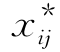（i＝1，2，3，4；j＝1，2，3）后，本问题的最优解由表3－26给出.

表3－25

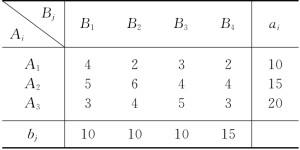
表3－26

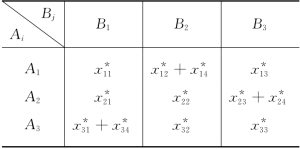
例3－10　（有界发量运输问题）　对表3－27给出的运输问题建立运输模型.

表3－27

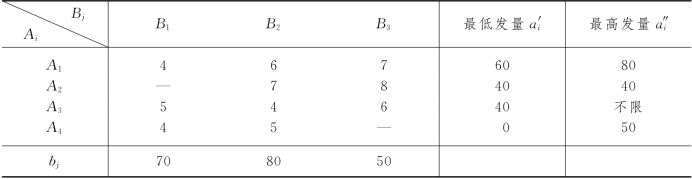
这样，我们得到运输模型，如表3－28所示.经计算，最优方案如表3－29所示.

表3－28

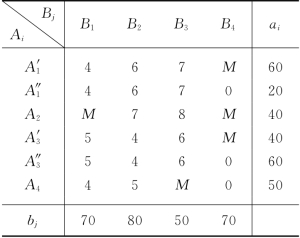
表3－29

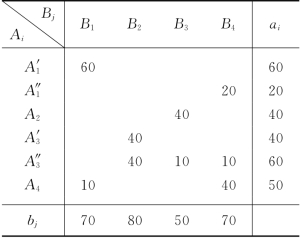
可见，A1实际发出60，由A1运至B1；A2的发量40由A2运至B3；A3实际发出90，A3至B2的运量为80，A3至B3的运量为10；A4实际发出10，由A4运至B1.

例3－11　（运量有界的运输问题）　表3－30给出一个运输问题.现在规定发点Ai至收点Bj的运量不能超过dij，由表3－31给定.试建立运输模型.

表3－30

表3－31

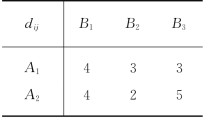
解　我们虚设Dij（i＝1，2；j＝1，2，3）6个点，Dij既作发点，又作收点，其发量及收量都为dij.

发点Ai的物资只可运送给Dij（j＝1，2，3），而Dij的物资只可运送给Bj，或者运送给自身.如果Ai至Dij的单位运价取为零，则Dij和Bj的单位运价就等于Ai至Bj的单位运价，于是，即得本问题的运输模型，如表3－32所示（表中未注明的单位运价都取充分大的正数M），其最优解由表3－33给出.

于是，本问题的最优运输方案为：A1发往B1，B2，B3的运量分别为3，3，2；A2发往B1，B2，B3的运量分别为4，2，4.

表3－32

表3－33

例3－12　（转运问题）　由表3－34给定一个运输问题.又物资可在A2，B2和B3处转运，A1与A2，B2与B1，B3与B1，B2与B3相互间单位运价分别为1，2，1和3.试建立运输模型.

表3－34

(www.daowen.com)

解　由于A2，B2和B3可以作为转运点，既可视为发点，又可视为收点，因此，整个问题可当作4个发点（A1，A2，B2和B3）和4个收点（A2，B1，B2和B3）的运输问题来处理.

由于原问题中A2无收量、B2和B3无发量，所以若建立运输模型，如表3－35所示，则转运运输不会发生.

我们对表3－35作如下修改：对表3－35中A2，B2和B3的发量和收量都加上一个较大的正数（比原问题表3－34所给的大的一个数），例如取100，则得本问题的运输模型如表3－36所示，此时，转运运输就会发生，最优解如表3－37所给.

表3－35

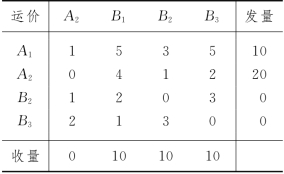
表3－36

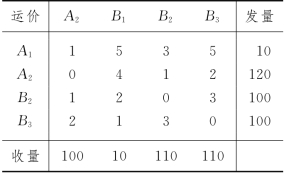
在表3－37所给的运输方案中，排除本地运输给本地的虚构物资运量，于是，本问题的具体运输方案为：

A1的发量10运至A2（于是A2有发量30）；A2的发量30分别运至B2和B3，运量分别为10和20；B3收到的运量为20，其中运量10转运至B1.

表3－37

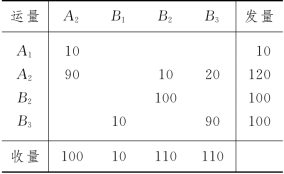
例3－13　（多品种物资运输问题）　若发点E1有某种原材料的一等品200，二等品300，发点E2有该种原材料一等品100，三等品150.收点F1将该种原材料供应给3类不同的消费部门：第一类部门可将这3种等级的原材料相互代用，共需150；第二类部门只能用一等品，需求量是50；第三类部门只用二等品或三等品，需求量是50.收点F2供应两类消费部门的需要：第一类部门使用一等品或二等品，需求量是200；第二类部门只用一等品，需求量是300.发点E1至收点F1，F2的单位运价分别为5，7；发点E2至收点F1、F2的单位运价分别为8，6.又设有一个该原材料的存储点Q，它的输出量与输入量及该原材料的等级均不受限制，Q点存储的原材料可以输往F1和F2，单位运价分别为6和9；E1和E2的原材料也可以输往Q点，单位运价分别为2和3.若F1和F2的需求量必须得到满足，E1和E2的原材料必须运走.试建立运输模型.

解　将E1拆为两个发点A1及A2，A1输出一等品200，A2输出二等品300；E2拆为两个发点A3及A4，A3输出一等品100，A4输出三等品150.同样地，将F1拆为3个收点B1，B2和B3，B1为收点F1的第一类消费部门，它对原材料的需求量为150，可以从A1，A2，A3和A4处运来；B2为F1的第二类消费部门，它的需求量为50，只能够从A1及A3处运来.为此，将A2及A4至B2的单位运价设为一个充分大的正数M；B3为F1的第三类消费部门，需求量为50，只能从A2及A4处运来，所以A1和A3至B3的单位运价视为M.F2拆为两个收点B4和B5，B4为F2的第一类消费部门，需求量为200，只能从A1，A2及A3处运来，于是A4至B3的单位运价设为M；B5为F2的第二类消费部门，需求量300，只可从A1及A3处运来，所以A2及A4至B5的单位运价取为M.

注意到本问题中，E1和E2具有的一等品总量为300，而对一等品的消费量至少需要350，所以一等品供应量不能满足需求量.由于本问题要求F1，F2的需求量必须得到满足，E1，E2的原材料必须运走，所以，让收发量及品种都无限制的存储点Q参加运输是必要的.我们将Q点拆为发点A5和收点B6.由于E1和E23种等级的原材料总供应量为750，故B6的需求量也设为750；F1和F2的总需求量为750，故A5的发量也设为750.考虑到A5的原材料仍可在原地（也即B6）存储，故设A5至B6的单位运价为零.结合题中所给的各收发点间的单位运价，可建立运输模型如表3－38所示，其最优解如表3－39所示.

表3－39中A5至B6的运量为700，事实上，这是虚设的.故本问题的最优运输方案为：E1输送二等品100给F1，输送一等品200和二等品200给F2；E2输送三等品100给F1，输送一等品100给F2，输送三等品50给Q点存储；Q点输送一等品50给F1.

表3－38

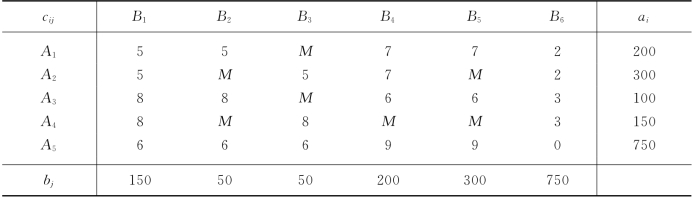
表3－39

例3－14　（空车调度问题）　有一辆汽车在A1，A2，A3，A4，A5，A6，A7和A88个地点之间运送4种物品，具体任务如表3－40所示：

已知Ai与Aj之间的距离为cij（单位：千米），试确定一个最优的汽车调度方案.

解　如果该辆汽车执行任务从Ai运送货物至Aj，此时会发生两种情况：

（1）若Aj还有数项任务未完成，那么汽车就任选一项任务从Aj驶往其到达点；

（2）若Aj已无货物需要运走，那么这辆空车从Aj开往哪一个地点去执行任务就成为我们应加以关注的问题.

因此，该辆汽车的最优调度，其目标就是使空车行驶的吨千米总数最少.

表3－40

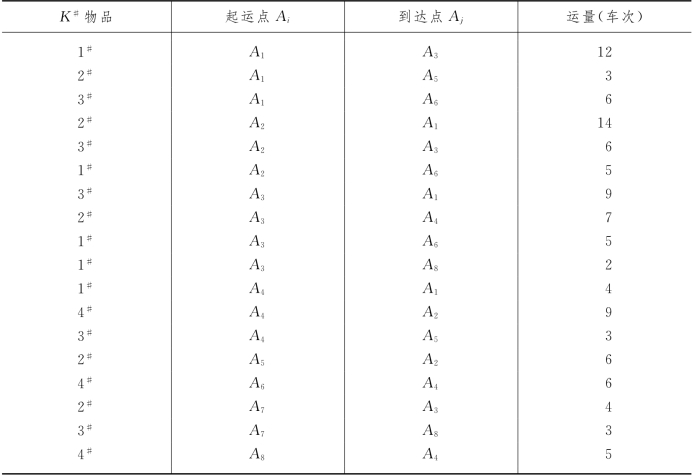
我们先列出Ai汽车出车数和来车数的平衡表如表3－41，表中“＋”号表示该点产生空车，“－”号表示该点需要调进空车.

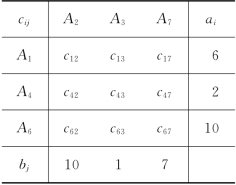
由表3－41可见，A1、A4和A6在运输过程中，可多出空车18车次，A2，A3和A7缺空车18车次.我们建立空车调度运输模型如表3－42.对表3－42用表上作业法求最优解，一旦发生情况（2）时，空车就按该最优解来进行调度.

表3－41

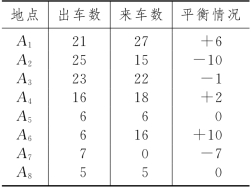
表3－42

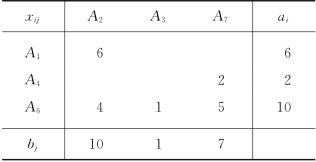
若是我们对表3－42中的各cij给出具体的数据，如表3－43所示，则得最优解如表3－44所示.

由表3－44可知：A1产生的空车开往A2有6车次；A4产生的空车开往A7有2车次；A6产生的空车开往A2有4车次、开往A3有1车次、开往A7有5车次.

表3－43

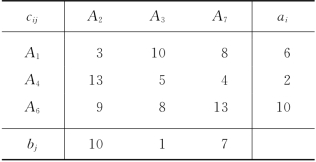
表3－44

例3－15　对例1－20所给的生产计划问题建立运输模型.

解　工厂每季生产产品可视为一个发点，可得4个发点A1，A2，A3和A4；Ai的发量即为工厂每季的生产能力ai.销售公司每季末需要一定数量产品，可视为4个收点B1，B2，B3和B4；Bj的收量即为表1－45中的需求量bj.

第i季度生产用于第j季度交货的每吨产品的实际成本被取为单位运价cij（j≥i），显然有cij＝di＋0.2（j－i）.又当j＜i时，是不可能发生Ai供货给Bj的，所以对应的cij取充分大的正数M.考虑到现在收发不平衡，有

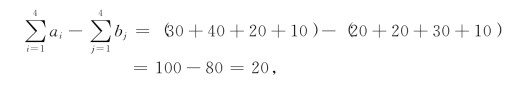
故虚设一个收点B5，其收量b5＝20，而ci5＝0（i＝1，2，3，4）.

这样，生产计划问题就化成了一个收发平衡的运输问题，其运输模型如表3－45所示.

表3－45