在求出运输问题的一个基本可行解和基本变量组Q以后,根据单纯形法步骤,我们应该计算变量xij的检验数rij.下面介绍位势法.
我们引进m+n个变量u1,…,um,v1,…,vn(其中有一个变量可以自由定值),对于xij∈Q,我们构造方程:
![]()
因为Q有m+n-1个基本变量,所以我们得到了m+n-1个方程.于是这m+n个变量中有一个变量可以自由定值,为了统一起见,我们不妨令u1=0.从而,由
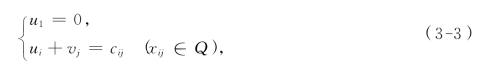
我们可以求出m+n-1个变量的值.我们把方程组(3-4)的一组解称为位势.
求出位势后,我们用下列公式来计算变量xij的检验数:
![]()
关于位势法的原理.我们这里就不作进一步说明了.
例3-6 对于表3-14,求出位势及检验数.
解 由于现在基本变量组
![]()
故根据式(3-3),得下面方程组:
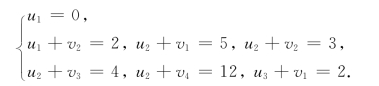
求得位势:
![]()
再由式(3-4)便可求得检验数rij,如表3-15所示,rij置于运输表格(i,j)格的左下角.运输表格中的ui列及vj行所填数值即位势ui和vj.
表3-15
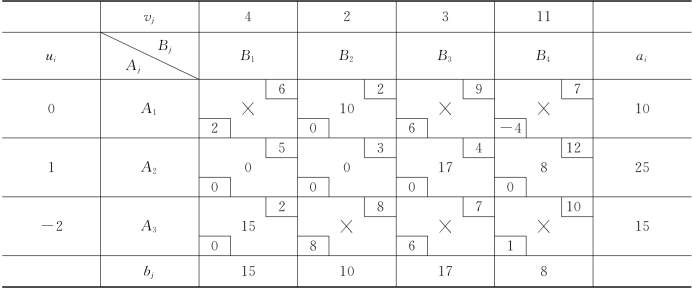
在手工计算时,当基本变量组Q确定以后,位势ui和vj及检验数rij都可在运输表格上直接计算而不必列出方程组及运算步骤.
例如,对于表3-15,现在u1=0,A1行中x12为基本变量,则由u1+v2=2而求得v2=2.对于B2所在列,x22为基本变量,对应一个方程u2+v2=3,求出u2=1,继续运算,求得全部位势及检验数.
下面我们来分析一下运输表格中检验数的实际背景.
例如,在表3-15中r14=-4,非基本变量x14对应的唯一闭回路为x14,x24,x22,x12,现在x14=0,A1处的物资不运输给B4.如果现在改变一下运输方案,把A1处的物资输送给B4一个单位,使x14=1,那么为了保持收发平衡,就要对x14对应的闭回路的另外3个顶点的运量依次进行调整:x24=8-1=7,x22=0+1=1,x12=10-1=9.这样的调整自然影响总运费:x14和x22增加运量一个单位,增加的运费为c14+c22=7+3=10;x24和x12减少运量一个单位,减少的运费为c24+c12=12+2=14,总运费减少c24+c12-c14-c22=14-10=4,它恰为r14的相反数.
由于r14=-4<0,对x14的闭回路的相应顶点运量调整一个单位可使总运费降低4个单位,现在min{x24=8,x12=10}=8,故调整量可取为8.调整后,我们让x14成为基本变量,x14=8,x24成为非基本变量,在(2,4)格打记号“×”,而x22=8,x12=2,如表3-16所示.
表3-16
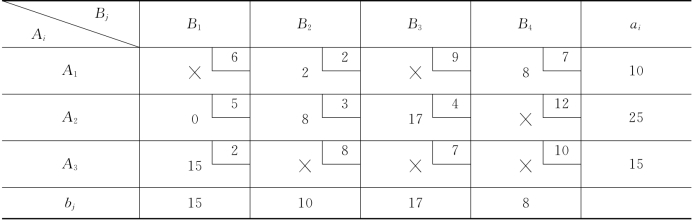
基于这一实例,我们将转轴规则总结如下.
若Q是问题(3-1)运输表格的一个基本变量组,xij(i=1,…,m;j=1,…,n)是相应基本可行解,如果相应检验数rij≥0(i=1,…,m;j=1,…,n)并不都成立,则选取rst满足:
![]()
取xst为进基变量.
在Q∪{xst}中,xst对应着一条唯一的闭回路E,不妨设xst为该闭回路的第一个顶点,其余顶点(都为基本变量)按某个方向顺序编号,记

取调整量d为
![]()
(若有数个xij满足此式,可任取一个为xpq),取xpq为出基变量.(https://www.daowen.com)
转轴以后的基本可行解X′为
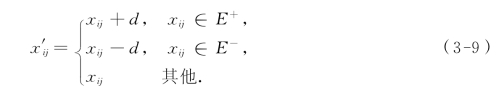
此时,基本变量组Q′=Q∪{xst}-{xpq}.X′的目标函数值f′0由式(1-36)知:
![]()
例如,在某运输问题的一张运输表格中,非基本变量x34的闭回路如图3-1所示,则
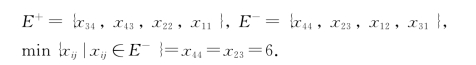
我们如果取x23为出基变量,则调整后,8个顶点对应的数值如图3-2所示.
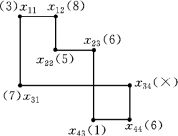
图3-1
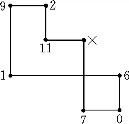
图3-2
下面列出位势法的算法步骤:
①应用西北角法或最小元素法求得初始基本可行解xij(i=1,…,m;j=1,…,n)和相应的基本变量组Q.
②由方程组u1=0;ui+vj=cij(xij∈Q),求得位势ui(i=1,…,m)和vj(j=1,…,n).
③计算rij=cij-ui-vj(i=1,…,m;j=1,…,n),取rst=min{rij|1≤i≤m;1≤j≤n}.
④rst=0?
若是,则xij(i=1,…,m;j=1,…,n)即为最优解,算法终止.
若否,则确定Q∪{xst}中的闭回路E以及E+和E-.
⑤取d=xpq=min{xij|xij∈E-}.
⑥取
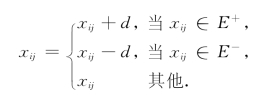
取Q=Q∪{xst}-{xpq},转步骤②.
例3-7 求解由表3-17所给出的运输问题(用最小元素法求初始基本可行解).
表3-17
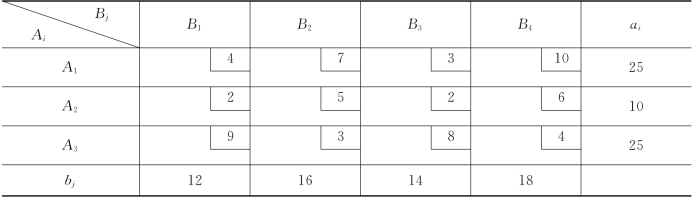
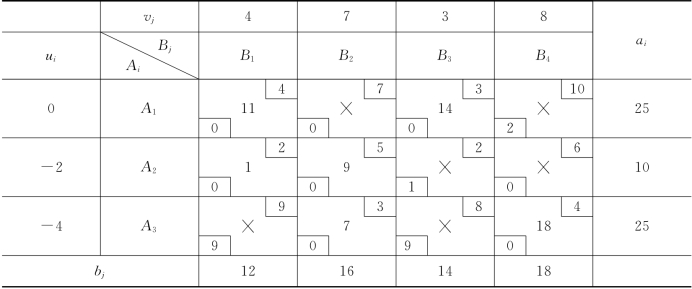
解 整个求解过程如表3-18、表3-19和表3-20所示.
表3-18
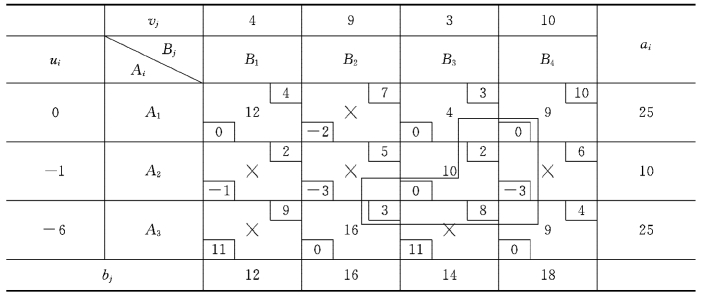
表3-19
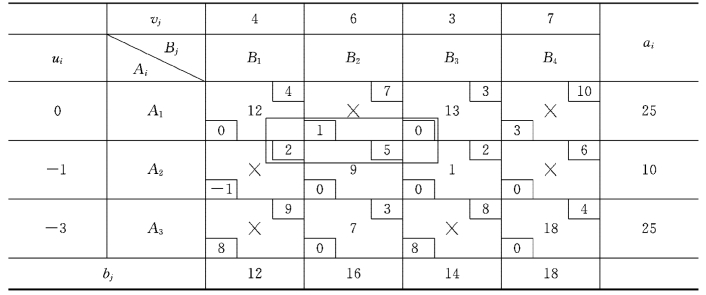
表3-20
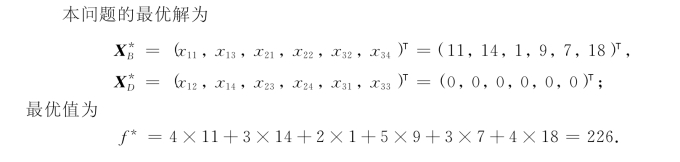
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







