求运输问题（3－1）的初始基本可行解有多种方法，这里介绍西北角法和最小元素法.

1.西北角法

西北角法按下列规则在mn个变量中选择m＋n－1个基本变量构成变量组Q：从运输表格的西北角x11开始，优先安排编号小的发点和收点之间的运输任务.

我们通过实例来说明西北角法.

例3－2　给出运输问题，如表3－6所示.试用西北角法确定它的一个基本可行解.

解　将变量xij所在方格记为（i，j），我们的目的是给各空格（i，j）填上xij的适当数量，使之满足发量约束或收量约束.在表3－7中，我们首先从西北角空格（1，1）开始填写：

表3－6

表3－7

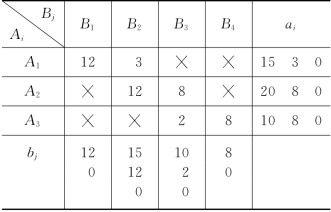
取Q＝｛x11｝.此时B1所需运量12全部从A1运来，B1对应的收量约束x11＋x21＋x31＝12已被满足，变量x21与x31都应取值为零，我们在相应空格（2，1）和（3，1）内打上记号“×”，表示该两个变量为非基本变量，其值为0.同时，b1由12变为0，a1变为15－12＝3.

接着，安排发点A1和收点B2之间的运输任务.取

于是此时A1的发量已全部运完，a1改为0，x13与x14作为非基本变量取值为0，在空格（1，3）和（1，4）内打上记号“×”，b2改为15－3＝12.于是，Q＝｛x11，x12｝.接下去再安排A2与B2之间的运输任务.如此继续进行运量分配，整个具体运算过程列在表3－7中，可知基本变量组Q＝｛x11，x12，x22，x23，x33，x34｝.

这样，得到一个基本可行解：

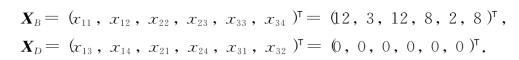
例3－3　对运输表格表3－8，用西北角法求初始基本可行解.

解　在表3－9中，取x11＝15，在（2，1）和（3，1）空格打记号“×”；取x12＝5，在（1，3）和（1，4）空格打上“×”，a1改为5，b1，b2分别改为0，10.

表3－8

表3－9

在表3－9中我们看到，当空格（2，2）填上数字x22＝10以后，发量约束和收量约束都得到满足，发量a2和收量b2都应变为0.此时，我们只能对行或列之一的剩余空格打记号“×”，然后在剩余空格中再按西北角法运算下去（否则，我们对行和列的剩余空格同时打记号“×”，那么运算结束时我们就会发现基本变量少于m＋n－1个）.

一般地，在算法的迭代过程中，如果对空格（s，t）填写数字xst后，发量约束和收量约束都得到满足，as与bt都变为0，则我们规定：

对Bt列的剩余空格打记号“×”，对空格（s，（t＋1））填写数字xs（t＋1）＝0（xs（t＋1）作为基本变量置入变量组Q中），再对As行剩余空格打记号“×”，然后继续运算下去.

按此规定，对表3－9继续运算，整个过程如表3－10所示.

本问题的基本可行解为

表3－10

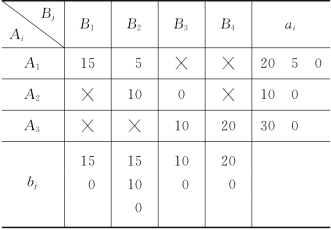
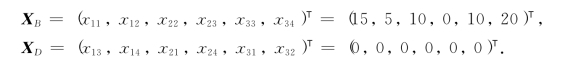
倘若，对例3－3，如果在表3－10中我们不选x23＝0作为基本变量，而让x23＝0作为非基本变量（用记号“×”表示），那么，我们应在其余非基本变量（表3－10中打记号“×”者）中选一个变量作为基本变量并取值为0，但要保证该变量置入变量组Q后，Q中不应含有闭回路.例如，我们可以选x14＝0作为基本变量置入变量组Q中.

在运算过程中，若以I表示当前还有货物要运送的发点的下标集合，J表示当前需求量尚未得到满足的收点的下标集合，Q为基本变量组，H为非基本变量组，则西北角法算法步骤如下：

①取I＝｛1，…，m｝，J＝｛1，…，n｝，Q＝∅.

②I是否仅含指标m？

若是，则xmj＝bj，j∈J.

Q＝Q∪｛xmj｜j∈J｝，H＝｛xij｜xij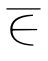Q，i＝1，…，m；j＝1，…，n｝；

xij＝0（xij∈H），算法终止.

若否，则转步骤③.

③J是否仅含指标n？

若是，则xin＝ai，i∈I.

Q＝Q∪｛xin｜i∈I｝，H＝｛xij｜xij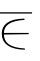Q，i＝1，…，m；j＝1，…，n｝；

xij＝0（xij∈H），算法终止.

若否，则确定s和t，取

s＝min｛i｜i∈I｝，t＝min｛j｜j∈J｝，转步骤④.

④取ε＝min｛as，bt｝，xst＝ε，Q＝Q∪｛xst｝.

⑤xst＝ε＝bt？(www.daowen.com)

若是，则bt＝bt－ε，as＝as－ε，J＝J－｛t｝，转步骤②

若否，则as＝as－ε，bt＝bt－ε，I＝I－｛s｝，转步骤②.

2.最小元素法

最小元素法采用如下规则选取m＋n－1个基本变量：优先安排单位运价cij小的发点Ai与收点Bj之间的运输任务.

例3－4　给出运输问题如表3－11所示.用最小元素法求初始基本可行解.

表3－11

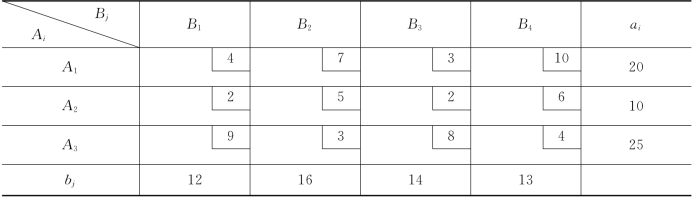
解　现在I＝｛1，2，3｝，J＝｛1，2，3，4｝，取cst＝min｛cij｜i∈I，j∈J｝＝c23＝2，于是，令

将x23置入变量组Q中，a2变为0，b3变为14－10＝4.对A2行的剩余空格打上记号“×”.

现在I＝｛1，3｝，J＝｛1，2，3，4｝，取cst＝min｛cij｜i∈I，j∈J｝＝c13＝3，于是，令

将x13置入变量组Q中，a1变为16，b3变为0.将B3列剩余空格打上记号“×”.继续运算，整个过程如表3－12所示.

表3－12

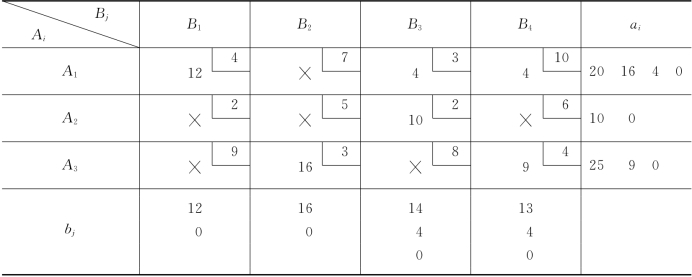
于是，得到一个基本可行解：

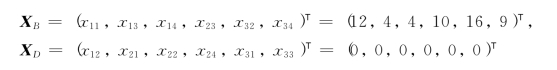
在运用最小元素法求基本可行解的过程中，为保证基本变量的个数为m＋n－1，我们要遵循下列两点规定：

①当运量待分配的运输表格剩下最后一行或最后一列有未填写数值或未打记号“×”的空格时，只准填写数值（包括零）不准打记号“×”；

②如果空格（s，t）填写数量值xst后，As行及Bt列的约束方程同时满足，修改后的as及bt均为0，我们仅对行或列之一的剩余空格打记号“×”.在这里，我们不妨规定对As所在行的剩余空格打记号“×”.

例3－5　给运输问题如表3－13所示，用最小元素法求初始基本可行解.

表3－13

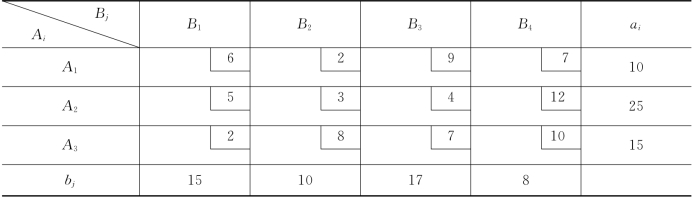
解　现在I＝｛1，2，3｝，J＝｛1，2，3，4｝，取cst＝min｛cij｜i∈J｝＝c12＝2，于是，令

a1与b2都变为0，对A1行的剩余空格打记号“×”.

现在I＝｛2，3｝，J＝｛1，2，3，4｝，cst＝min｛cij｜i∈I，j∈J｝＝c31＝2，于是，令

a3与b1均变为0，对A3行剩余空格打记号“×”.

表3－14

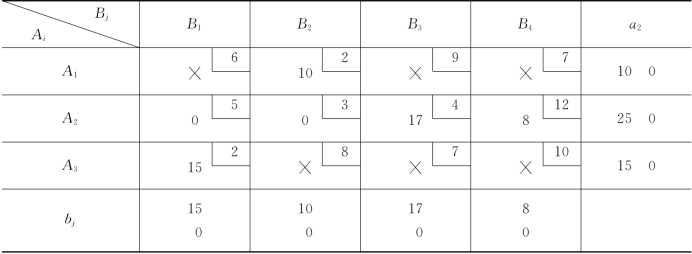
此时，I＝｛2｝，J＝｛1，2，3，4｝，我们对A2行的空格均填写数字：x2j＝bj.整个运算过程如表3－14所示.

由表3－14得基本可行解：

我们将最小元素法算法步骤归纳如下：

①取I＝｛1，…，m｝，J＝｛1，…，n｝，Q＝∅.

②I是否仅含一个指标？

若是，则对i∈I，取xij＝bj（j∈J）.Q＝Q∪｛xij｜j∈J｝，转步骤③.

若否，则J是否仅含一个指标？

若是，则对j∈J，取xij＝ai（i∈I），Q＝Q∪｛xij｜i∈I｝，转步骤③.

若否，则转步骤④.

③取非基本变量组H＝｛xij｜i＝1，…，m；j＝1，…，n｝－Q；对xij∈H，令xij＝0，算法终止.

④取cst＝min｛cij｜i∈I，j∈J｝；xst＝min｛as，bt｝，Q＝Q∪｛xst｝，as＝as－xst，bt＝bt－xst.

⑤as＝0？

若是，则I＝I－｛s｝，转步骤②.

若否，则J＝J－｛t｝，转步骤②.