运输问题这个名称的获得是因为这类模型首先在物资运输的合理规划中形成并运用的缘故.但是，运输问题及其求解方法所管辖、研究的对象事实上要广义得多，例如，对于生产计划等这类管理问题它也是行之有效的.下面我们给出一般的运输问题的数学模型：

例3－1　现有m个发点A1，…，Ai，…，Am，可供应某种物资给n个收点B1，…，Bj，…，Bn.发点Ai的物资供应量（发量）为ai，收点Bj对物资的需求量（收量）为bj，且收发平衡：即.又设单位物资从Ai运往Bj的单位运价为cij.问怎样运输这些物资，以使总运费最小？

解　我们将问题所给的有关信息制成表3－1，并称它为运输收发平衡单位运价表（有时简称运输表格）.

表3－1

设发点Ai至收点Bj的运量为xij，则我们有表3－2.

表3－2

我们不难建立运输问题的线性规划模型：

我们知道，单纯形法的基本步骤是：寻找初始基本可行解，由检验数来判别它是不是最优解？若不是最优解，则进行转轴.对于运输问题来说，这些步骤可采用简单方法.在手算时，它们可在运输表格上直接进行，所以俗称运输问题的求解方法为表上作业法.

那么，我们在运输收发平衡表的mn个变量中，如何选取m＋n－1个变量使其成为基本变量组呢？为此，我们先介绍一些有关的基本概念.

（1）设E是运输问题（3－1）的一组变量.如果对E中变量作适当的排列后能得到下列形式：

其中i1，i2，…，is互不相同，j1，j2，…，js互不相同，则称E为运输问题（3－1）的一个闭回路.闭回路中相应变量称为闭回路的顶点.

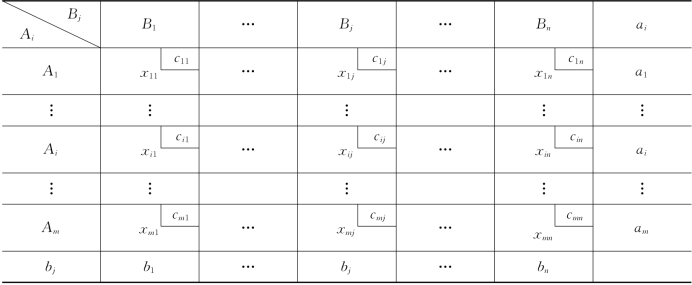
例如，设m＝3，n＝4，E＝｛x13，x14，x34，x31，x21，x23｝是一个闭回路.若把闭回路中变量作为顶点在运输表格中画出，并把闭回路中处在同一行或同一列的顶点用线段相连（称为闭回路的边），那么，上述E就有表3－3所示的形状.

表3－3

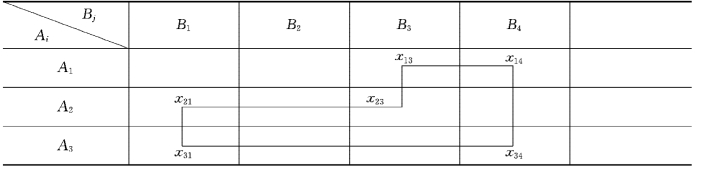
闭回路的边只能是水平或垂直的，闭回路的边所通过的行或列都恰有它的两个顶点.

（2）设Q是运输问题（3－1）的一组变量，若xij为Q中一个变量，且xij是第i行或第j列中属于Q的唯一变量，则我们称xij为Q的一个孤立点.(www.daowen.com)

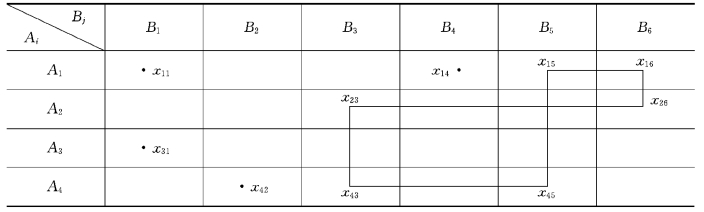
例如，如表3－4所示，在变量组

中，x31，x14和x42是Q的孤立点.E＝｛x15，x16，x26，x23，x43，x45｝是一个闭回路，E的顶点都在Q中，我们称E为Q中的一个闭回路.

表3－4

对于运输问题（3－1），我们给出下列定理.

定理3－1

（1）在运输问题（3－1）的m＋n个等式约束方程中只有m＋n－1个方程是相互独立的，而且其中任意一组m＋n－1个约束方程都是相互独立的.

（2）在运输问题（3－1）的mn个变量中，选取m＋n－1个变量构成变量组Q，则Q能成为基本变量组的充要条件是：Q中不存在闭回路.

（3）设Q是运输问题（3－1）的一组基本变量，xst为非基本变量，则xst必对应一条唯一的闭回路E.E除顶点xst外，其余顶点都为基本变量.

（4）如果在运输问题（3－1）中ai（i＝1，…，m）和bj（j＝1，…，n）都为整数，则任一基本解中各变量的取值均为整数.例如，表3－5所给的变量组

就是一个基本变量组.此时，x11为非基本变量（今后用记号“×”表示），则可见在Q∪｛x11｝中就存在一条闭回路E＝｛x11，x15，x45，x41｝.

表3－5

下面我们来讨论一下，若Q为运输问题的一个基本变量组，xst为非基本变量，那么，我们如何在Q∪｛xst｝中确定闭回路E呢？

从闭回路的性质可知，Q∪｛xst｝中的孤立点xij一定不是E的顶点，故我们可以通过反复从变量组中删去孤立点来获得E.有的变量原来并不是一个孤立点，但当从变量组中删去一些变量后，就可能成为由余下变量组成的变量组的孤立点，它同样应被删去.最后剩下未被删去的变量便组成闭回路E，而xst一定是E的一个顶点.

例如，在表3－5中，对于Q∪｛x11｝来说，现在x12，x14，x26，x35是孤立点，但从Q∪｛x11｝中删去这4个点以后得Q1，则x23成为Q1的孤立点，从Q1中删去x23得Q2，则x43又成为Q2的孤立点，再从Q2中删去x43，得E＝｛x11，x41，x45，x15｝，它是一个闭回路.