例2－23　如果对于例2－22中的模型（P）（2－34），b1与b2分别代表两个车间的劳动工时（一周），假定每个工人一周工作40小时，现在准备从第二个车间抽调θ个工人到第一个车间，问怎么求解？

解　现在向量b发生了变化：

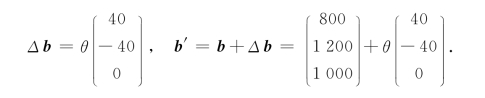
此时，向量b各分量为θ的函数，我们称该线性规划为参数规划.

根据本问题的实际背景，应该有b′≥0，即应有800＋40θ≥0，1 200－40θ≥0.所以，我们只要对θ∈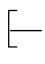20，30］的情况进行讨论就可.

表2－23对应的XB＝（x5，x4，x2）T，基B＝（A5，A4，A2），由表2－23可知其对应的B－1如

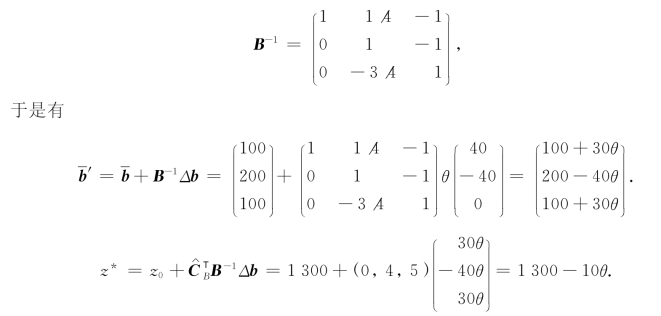
于是表2－23变成为表2－30.

表2－30

要使最优基保持不变，则要求下列条件必须成立：

可知，当θ∈［－10／3，5］时，X＊＝（0，100＋30θ，0，200－40θ）T，z＊＝1 300－10θ.

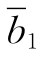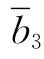（1）如果θ＝－10／3，在表2－30中，＝0或者＝0，运用对偶单纯形法，x5或者x2都可以作为出基变量.今选择x5为出基变量，x3为进基变量，取y13＝－13／4为枢轴元素进行转轴，得到表2－31.

表2－31

要使最优基保持不变，则要求下列必须条件成立：

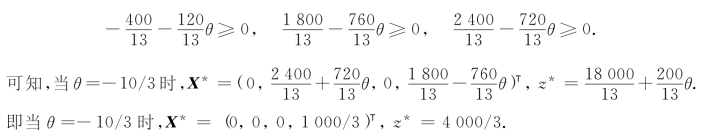
（2）如果θ＝－10／3，则在表2－31中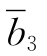＝0，运用对偶单纯形法，选择x2作为出基变量，x6为进基变量，取y36＝－7／13为枢轴元素进行转轴，得到表2－32.

表2－32

要使最优基保持不变，则要求下列条件成立：

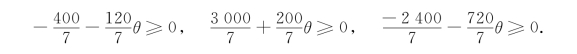
可知，当θ∈［－15，－10／3］时，

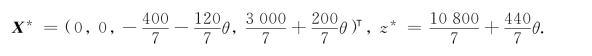
（3）如果θ＝－15，则在表2－32中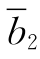＝0，选择x4作为出基变量，x7为进基变量，y26＝－1为枢轴元素进行转轴，得到表2－33.(www.daowen.com)

表2－33

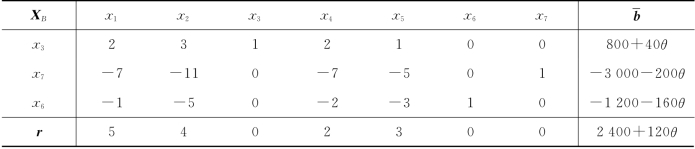
要使最优基保持不变，则要求下列条件成立：

可知，当θ∈［－20，－15］时，X＊＝（0，0，800＋40θ，0）T，z＊＝2 400＋120θ.

（4）如果θ＝5，在表2－30中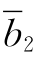＝0，运用对偶单纯形法，选择x4作为出基变量，x7为进基变量，取y27＝－1为枢轴元素进行转轴，得到表2－34.

表2－34

要使最优基保持不变，则要求下列条件成立：

可知，当θ∈［5，30］时，X＊＝（0，300－10θ，0，0）T，z＊＝1 500－50θ.

（5）我们再指出，若是在步骤（1）中，如果θ＝－10／3，则在表2－30中，因为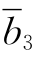也为0，所以也可以不选择x5为出基变量，而是选择x2作为出基变量，则取x6为进基变量，在表2－30中取y36＝－3／4枢轴元素进行转轴，得到表2－35.

表2－35

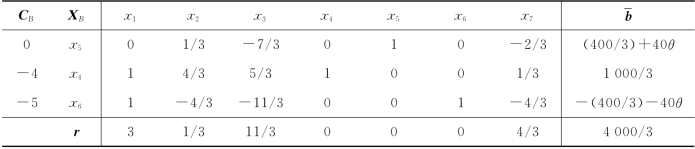
要使最优基保持不变，则要求下列条件成立：

可知，当θ＝－10／3时，X＊＝（0，0，1 000／3，0）T，z＊＝4 000／3.

总结上面的求解过程，我们得到表2－36.

表2－36

从表2－36可以看出，在区间Ⅰ，Ⅱ，应使θ尽可能大，以使z实现最大，即θ取区间的右端点；在区间Ⅳ与Ⅴ，应使θ尽可能地小，以使z实现最大，即θ取区间的左端点.这样得到6个参数区间的最大利润（见表2－37）.

表2－37

本问题的答案是要获得最大利润，必须将3.33个工人从车间Ⅰ调到车间Ⅱ.