如果一个单位的资源b1的成本变动θ，则目标函数就要发生变化，这在日常生产活动中是经常发生的，于是，一个静态的线性规划问题就成为动态问题.根据模型第一个约束条件中4个产品的资源消耗系数a1j（j＝1，…，4），可知模型（2－34）的目标函数改变为

此时，由于目标函数z作为参数θ的函数（即向量C中各分量含有参数θ），我们把该线性规划称为参数规划.

下面我们来讨论最优解X＊与θ之间的关系.

（1）由于θ的引入，表2－23修改成为表2－24.

表2－24

如果希望最优解不变，则要求非基本变量的检验数非负，下列条件必须成立：

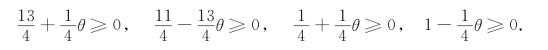
可知：当θ∈［－1，11／13］时，有

当θ＝－1或者11／13时，检验数r6＝0或者r3＝0，基本最优解不唯一.

（2）如果θ＝－1，在表2－24中r6＝0，运用单纯形法，对表2－24选择x6为进基变量、x4为出基变量、取y26＝1作为枢轴元素进行转轴，得到表2－25.

表2－25

如果希望最优解不变，则要求下列条件成立：

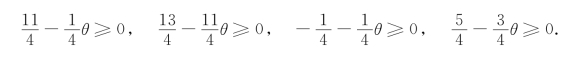
可知，当θ∈（－∞，－1］时，X＊＝（0，250，0，0）T，z＊＝1 250－750θ.

（3）如果θ＝11／13，在表2－24中r3＝0，运用单纯形法，对表2－24选择x3为进基变量、x2为出基变量、取y33＝11／4作为枢轴元素进行转轴，得到表2－26.

表2－26

如果希望最优解不变，则要求下列条件成立：

可知，当θ∈［11／13，11／7］时，有

(www.daowen.com)

（4）如果θ＝11／7，在表2－26中r6＝0，运用单纯形法，对表2－26选择x6为进基变量、x4为出基变量、取y26＝5／11作为枢轴元素进行转轴，得到表2－27.

表2－27

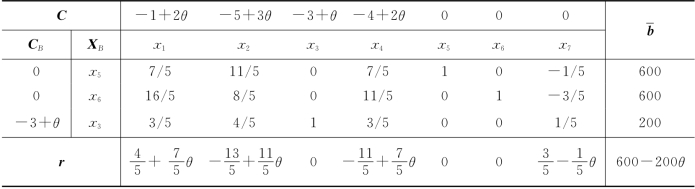
如果希望最优解不变，则要求下列条件成立：

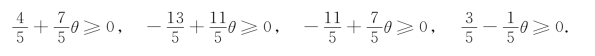
可知，当θ∈［11／7，3］时，X＊＝（0，0，200，0）T，z＊＝600－200θ.

如果θ＝3，在表2－27中，r7＝0，运用单纯形法，对表2－27选择x7为进基变量、x3为出基变量、取y37＝1／5作为枢轴元素进行转轴，得到表2－28.

表2－28

如果希望最优解不变，则要求下列条件成立：

可知，当θ∈［3，－∞）时，X＊＝（0，0，0，0）T，z＊＝0.

总结上面的求解过程，我们得到表2－29.

表2－29

从表2－29看出，在θ＝－2时，z＊＝2 750；θ＝－1，z＊＝2 000；θ＝0，z＊＝1 300；θ＝1，z＊＝618.在实际问题中，θ的取值不可能在θ∈（－∞，＋∞）内变化，视具体问题而定.

通过这个例子，我们得到了C中各分量含有参数θ时的参数规划求解的基本方法，读者可根据不同的例题不同的要求仿照此方法进行求解.

向量C各分量为参数θ函数的参数规划，在参数θ变化时，关于最优解可有如下结论：

（－∞，＋∞）分为多个关联的参数区间，同一个参数区间有同一个最优解，在区间的端点上有多个基本最优解.这些端点被称为特征点.

也可能发生下面3种情况：

（1）（－∞，a］分为多个关联的参数区间，在（a，＋∞）上无解；

（2）［a，＋∞）分为多个关联的参数区间，在（－∞，a）上无解；

（3）［a，b］分为多个关联的参数区间，在（－∞，a）与（a，＋∞）上无解.