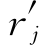如果cs在某个范围内摄动，这将影响原来问题最优表T（B）中r行的元素.设＝cs＋Δcs，我们的问题是：cs或Δcs在何范围内变动，基本最优解不发生变化，也即新的检验数≥0（j＝1，…，n）仍应成立.我们先来看一个例子.

例2－13　对例2－12，（1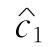）在何范围内变化，最优基不变？若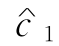＝4，求最优解.（2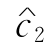）在何范围内变化，最优基不变？若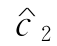＝9，求最优解.

解　（1）在最优表表2－10中，x1为非基本变量，当c1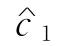＝－变动时，CB没有改变，故受影响的仅是最优表中检验数r1.此时

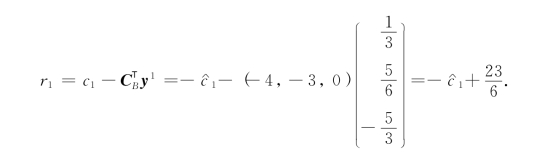
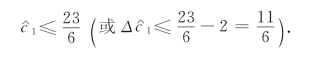
要使最优基保持不变，应有r1≥0，即换言之，只要1＃产品的单位产品利润不超过23／6，则生产1＃产品就是不经济的.

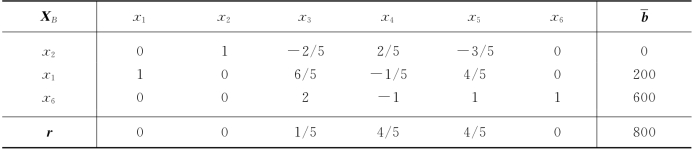
若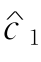＝4，则r1＝－4＋23／6＝－1／6，于是，目前的生产计划就不是最优.我们将表2－10修改成表2－11，用单纯形法继续迭代，得表2－12，即得最优解X＊＝（200，0，0）T，最优值z＊＝800.

表2－11

表2－12

（2）在表2－10中，x2为基本变量，当c2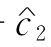＝－摄动时，CB改变，故最优表中非基本变量x1，x4，x5的检验数r1，r4，r5都要改变，我们把r1，r4和r5表示成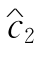的函数：

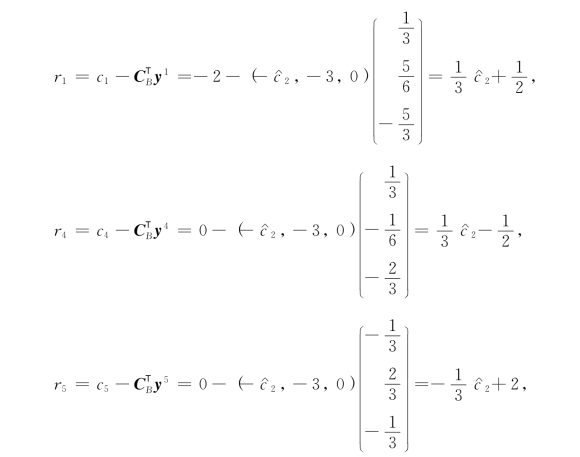
为使最优基不变，则r1，r4和r5都应非负，即

表2－13(www.daowen.com)

表2－14

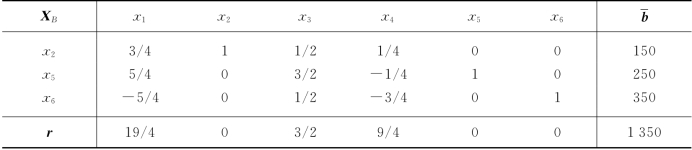
在上述例子的基础上，下面我们给出参数cs灵敏度分析的一般公式.

1.情况一

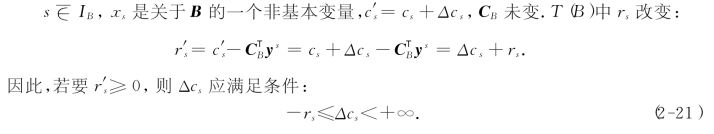
2.情况二

s∈IB，xs为关于基B的一个基本变量，不妨设s＝Bi，此时CB有了变化：

因此，T（B）中的f0和rj（j∈ID）都将受到影响：

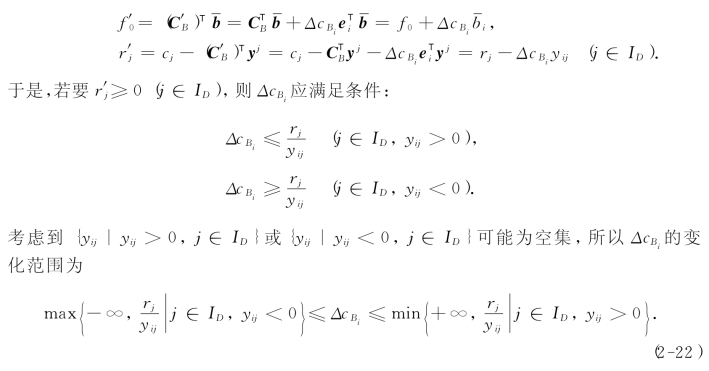
（在上述不等式中，若界为－∞或＋∞，则相应的“≤”应改为“＜”，下面类似的情况不再说明）.

综上所述可知，如果Δcs没有超出式（2－21）或式（2－22）所给的范围，那么最优基和最优解不变.如果Δcs超出规定的范围，则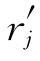≥0对j＝1，…，n不全成立，可将最优表中原r行元素修改后用单纯形法继续迭代，求得新的最优解.