例2－12　某工厂生产3种产品，有关信息如表2－9所示.问如何安排生产计划，使工厂获得最大利润？

表2－9

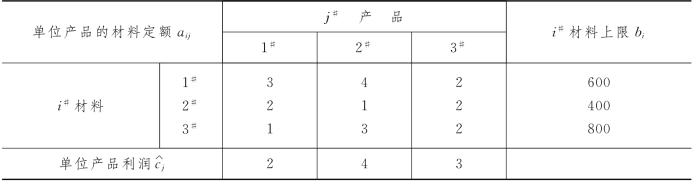
解　设产品j＃的产量为xj，则得线性规划模型：

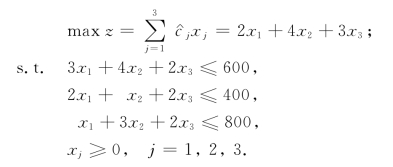
将它化成标准型（LP）：

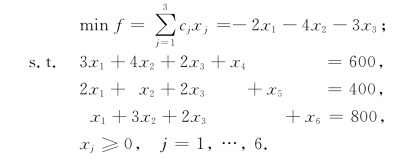
用单纯形法求解（LP），得最优单纯形表如表2－10所示.

表2－10

(www.daowen.com)

最优解X＊＝（x1，x2，x3）T＝（0，200／3，500／3）T，最优值z＊＝2 300／3.

这个最优解是在参数cj，bi，aij都固定不变的条件下取得的.但是，在实际问题中，对一个具体的企业来说，参数cj，bi，aij不是固定不变的.例如，产品的市场价格可能有所变动；国家分配的原材料可能有所增减；动力供应情况可能随季节而变化；添置新设备而使生产台时增加；由于产品设计结构有所改进，使单位产品的原材料消耗定额有所增减……现实诸因素的种种变化都会引起已建立的数学模型的参数变化.或者，当运用线性规划编制完生产计划并即将付诸应用时，又发生了新的情况，某些原来未加限制的资源现在有了限制，从而出现一个新的追加约束条件.或者，企业准备增加新产品，使工厂的生产计划发生整个变化.

因此，我们面临这样的问题：上述种种情况的发生，将对已求得的最优解产生什么影响？或者说，我们如何在原有的最优单纯形表的基础上用最少的计算量，去获得修改后的线性规划问题的最优解？这就是下面我们要讨论的灵敏度分析问题.

假设线性规划（LP）的基本最优解＝0，最优基为B，指标集IB＝｛B1，…，Bm｝，我们分下面几个问题来进行灵敏度分析：

（1）变量xs的目标函数系数cs在何范围内变动，问题（LP）的最优基（最优解）不变？如果超出这个范围，如何求最优解？

（2）第s种资源bs在何范围内变动，最优基不变？如果bs超出这个范围，如何求最优解？

（3）变量xs在矩阵A中的系数列向量A.s发生变化，如何求新问题的最优解？

（4）追加新的约束条件，如何求新的线性规划的最优解？

（5）增加新的变量xs，如何求新问题的最优解？