对偶理论告诉我们，在原有问题和对偶问题的最优解之间存在着密切的关系.有时，我们可以从求解原有问题的最优单纯形表中，得到对偶问题的最优解.

1.情况一

如果我们考虑的原有问题（P）为下列线性规划：

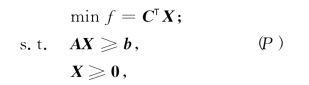
它的标准型（LP）为

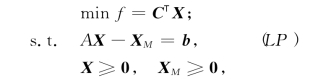
其中XM＝（xn＋1，…，xn＋m）T.

显然，（P）与（LP）的对偶问题是同一个线性规划（D）：

若用单纯形法求解（LP），得最优基B和最优单纯形表T（B）.对（LP）来说，当j＝n＋i（i＝1，…，m）时，有A.j＝－ei，cj＝0，因此

从而，在最优表中，有

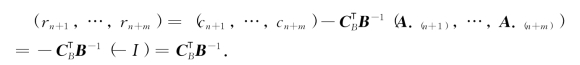
根据定理2－3（4）（对偶性定理）可知：

也就是说，在（LP）的最优单纯形表中，剩余变量对应的检验数（rn＋1，…，rn＋m）T即为最优单纯形因子，它是对偶问题的最优解U＊.

同时，在最优单纯形表T（B）中，还有

例2－9　用对偶单纯形法求解下列线性规划（P）：

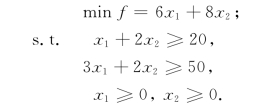
解　它的标准型（LP）为

用对偶单纯形法求得最优单纯形表如表2－7所示.

表2－7

（P）和（LP）的对偶问题（D）为

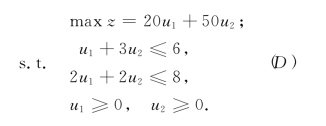
由表2－7可知，（D）的最优解为

此时，表2－7对应的最优基

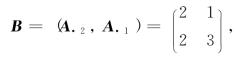
由表2－7知，最优基B的逆矩阵

2.情况二(www.daowen.com)

如果我们考虑的原有问题（P）为

也就是说，在（LP）的最优单纯形表T（B）中，松弛变量对应的检验数（rn＋1，…，rn＋m）T，即为最优单纯形因子，它是对偶问题（D）的最优解U＊.

同时，在（LP）的最优单纯形表T（B）中，还有

例2－10　用单纯形法求解下列线性规划（P）：

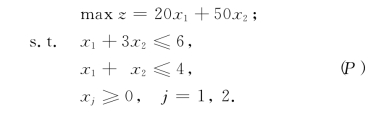
解　它的标准型（LP）为

用单纯形法求得（LP）的最优单纯形表如表2－8所示.

表2－8

（P）的对偶问题（D）为

由表2－8可知，（D）的最优解

此时，表2－8对应的最优基

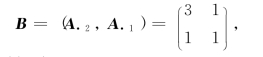
由表2－8可知，最优基B的逆矩阵

3.情况三

如果我们考虑一般形式的线性规划.首先将它化为标准型，然后用大M法进行求解.假设初始指标集IB和初始基分别为

例2－11　假设例1－14所给的线性规划为（P），试利用在大M法求解过程中的相关信息，给出对偶问题的最优解.

解　在用单纯形法求解它的（LPM）问题时，初始单纯形表为表1－22，初始指标集IB＝｛6，5，7｝；最优单纯形表T（）为表1－24，最优基＝（A.1，A.5，A.2），指标集＝｛1，5，2｝.

由此可知（P）的对偶问题的最优解

同时，由表1－24可知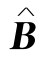的逆矩阵为

如果我们计算最优单纯形因子，则

可见，与上述结果相同.