我们现在对标准型线性规划（LP）：min｛CTX｜AX＝b，X≥0｝及其对偶问题（LD）：max｛bTU｜ATU≤C，U≷0｝之间的关系进行讨论，其结论对一般形式的线性规划（P）及其对偶问题（D）同样适用.我们记（LP）的可行域为KLP，记（LD）的可行域为KLD.

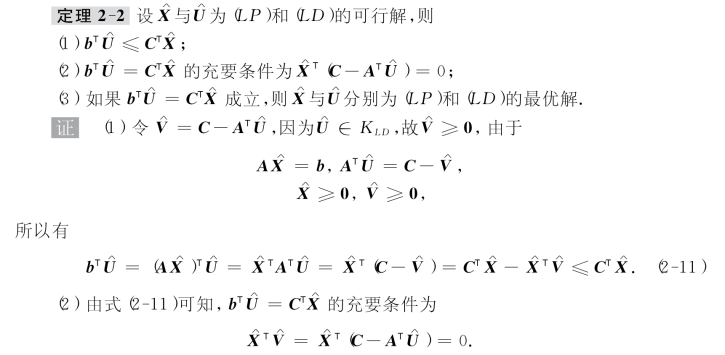
（3）设X为（LP）的任一可行解，由式（2－11）可知：

因此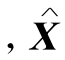为（LP）的最优解.同理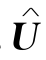，为（LD）的最优解.

定理2－3　（对偶性定理）

（1）若（LP）有可行解，但目标函数值在可行域上无下界，则（LD）不可行；

（2）若（LD）有可行解，但目标函数值在可行域上无上界，则（LP）不可行；

（3）（LP）和（LD）同时有最优解的充要条件为它们同时有可行解；

（4）若应用单纯形法求解（LP），得基本最优解X＊，相应最优基为B，则单纯形因子为（LD）的最优解，且CTX＊＝bTU＊；

（5）若（LP）有最优解X＊，则（LD）必有最优解U＊存在，且CTX＊＝bTU＊；

（6）若（LP）有可行解，（LD）无可行解，则（LP）的目标函数值在可行域上无下界；

（7）若（LD）有可行解，（LP）无可行解，则（LD）的目标函数值在可行域上无上界.

证　（1）反之，若（LD）有可行解U∧存在，则任X∈KLP，都有，这与（LP）在KLP上无下界矛盾，故（LD）不可行.

（2）与（1）的证明类似.

（3）必要性是显然的，故只需证充分性.

若（LP）有可行解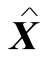，（LD）有可行解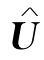，则对任意X∈KLP，都有CTX≥bT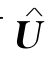，故（LP）的目标函数值在KLP上有下界，所以（LP）有最优解.类似地可证（LD）有最优解.

（4）由于在最优基B的单纯形表T（B）中

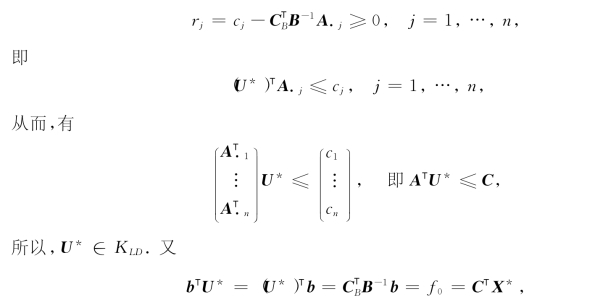
由定理2－2（3）可知U＊是（LD）的最优解，且CTX＊＝bTU＊.

（5）由于（LP）有最优解X＊，根据定理1－1，（LP）一定有基本最优解.由本定理（4）可知（LD）必有最优解U＊存在，且CTX＊＝bTU＊.

（6）反之，（LP）有最优解，则由本定理（5）可知（LD）应有最优解，与（LD）无可行解矛盾，故（LP）在KLP上无下界.

（7）与（6）的证明类似.(www.daowen.com)

原有问题和对偶问题解之间的对应关系，除了定理2－3告诉我们的各种情况外，也可能两个问题都不可行.例如，下列原有问题（P）和其对偶问题（D）都不可行：

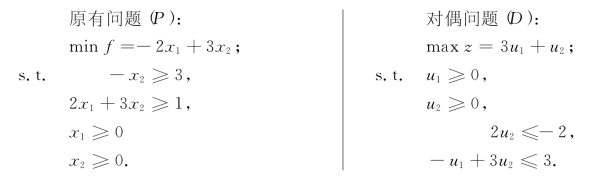
综合上述讨论可见，一组对偶规划的解之间只有下列3种情况：

（1）两个规划都有最优解，且最优值相等；

（2）两个规划都不可行；

（3）一个规划不可行，另一个规划有可行解，但最优解不存在.

原有问题（P）和对偶问题（D）的解之间的关系我们可用表2－1来说明.

表2－1

例2－5　用对偶理论讨论下述一组对偶规划：

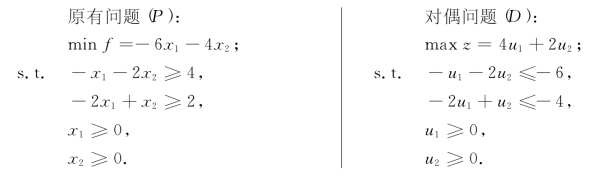
解　显然，（u1，u2）T＝（6，0）T是（D）的一个可行解，而（P）的约束条件－x2－2x2≥4在第一象限是不可能实现的，（P）无可行解.所以，由定理2－3（7）可知，（D）在可行域上无上界.

由定理2－2（2）和（3）可知，当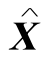和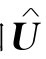分别为（LP）和（LD）的可行解时，则它们都是最优解的充分必要条件为

同时，对于（LP）和（LD）来说，显然有

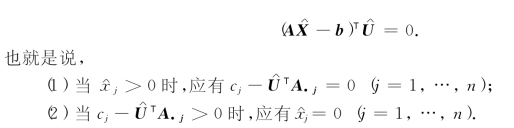
现在，我们将该结论推广到一般形式的一组对偶规划（P）和（D）上，而得到松弛互补定理.为了更好地理解该定理，我们再次列出（P）和（D）：

对照（P）和（D）的定义，可见，松弛互补条件反映了（P）中变量（或约束条件）与（D）中对应的约束条件（或变量）在最优情况下相互之间的制约关系：

例2－6　给定一组对偶规划：