我们考虑下述一个线性规划问题.

例2－1　（营养问题）　某养鸡场所用的混合饲料由n种天然饲料配合而成.要求在这批配合饲料中必须含有m种不同的营养成分，且第i＃种营养成分的含量不低于bi.已知第i种营养成分在每单位第j＃种天然饲料中的含量为aij，第j＃种天然饲料每单位的价格为cj.试问，应如何对这n种饲料配方，使这批饲料的费用最小？

解　设xj为第j＃种天然饲料的用量.

显然，aijxj即为所用第j＃种天然饲料中第i＃种营养成分的含量为这批混合饲料中第i＃种营养成分的总含量，它不应低于bi.于是，我们得下列线性规划模型：

现设想有一个饲料加工厂欲把这m种营养成分分别制成m种营养丸：

设第i＃种营养丸的价格为ui（i＝1，…，m）.则养鸡场采购一个单位的第j＃种天然饲料，就相当于对这m种营养丸分别采购数量a1j，…，amj，所花费用为.养鸡场自然希望在用营养丸代替天然饲料时，在价格上能相对地比较便宜，故而饲料加工厂为了能与天然饲料供应者竞争，在制订价格时必然满足下述条件：

另一方面，养鸡场如果全部采购营养丸来代替天然饲料进行配料，则第i种营养丸就需采购bi个单位，所花费用为biui，总费用为z＝

饲料加工厂面临的问题是：应把这m种营养丸的单价ui（i＝1，…，m）定为多少，才能使养鸡场乐意全部采用该厂生产的营养丸来取代这批天然饲料，且使本厂在竞争中得到最大收益.为该问题建立数学模型，即得如下线性规划：

若令U＝（u1，…，um）T，该问题即为

例2－2　写出下列线性规划问题（P）的对偶问题（D）：

解　首先把它化成模型（2－1）的形式：

令x2＝，得（P）：

根据上述（P）的对偶问题的定义，我们即可给出它的对偶问题：

若令u1＝v1－v2，则上述问题即为

如果我们来分析一下它们之间的对应关系：

可见，在对偶问题（D）中，原有问题（P）中的等式约束对应的变量u1为自由变量，（P）中的自由变量x2对应的约束条件为等式约束.在此基础上，我们给出一般线性规划（P）的对偶问题（D）的定义：

其中指标集

也就是说，由原有问题（P）构造对偶问题（D）的一般规则为：(www.daowen.com)

（1）在原有问题（P）中，目标函数为求min f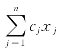＝，其约束条件统一成≥或＝.

（2）在对偶问题（D）中，目标函数为求max z＝.

（3）在原有问题（P）中与bi相应的一个约束条件，对应着对偶问题（D）的一个变量ui：如果该约束条件为不等式，则ui≥0；如果该约束条件为等式，则ui为自由变量.

（4）原有问题（P）的每个变量xj对应着对偶问题（D）的一个约束条件：如果（P）中xj≥0，则（D）中为≤cj；如果xj≷0，则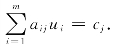

我们称问题（P）和问题（D）为一组对偶规划.

如果在原有问题（P）（2－5）中无不等式约束（即取M1＝∅），且无自由变量（即取N2＝∅），则（P）就是标准型线性规划（LP）.此时，得到这样一组对偶规划：

定理2－1　对偶问题（D）的对偶问题即为原有问题（P）.

证　现将定义中的对偶问题（D）（2－6）变换成下列等价形式：

把它视为原有问题，根据定义它的对偶问题为

易知，它等价于原有问题（P）（2－5）.

该定理告诉我们，可以把（P）和（D）中的任何一个视为原有问题，那么，另一个问题就是它的对偶问题，它们是互为对偶的.

例2－3　写出下列问题的对偶问题：

解　首先我们对该问题进行整理.将2x1＋＋x3≥1变换为－2x1－－x3≤－1，并令＝－x2（x2≥0），得（P）：

它的对偶问题（D）为

例2－4　写出下列问题（P）的对偶问题：

解　（P）可以写成：

它的对偶问题（D）为