线性规划是运筹学中应用最为广泛的一个主要分支,但是,我们不可能用大量的篇幅去讨论生产实践中的大型问题,而只能列举一些类型不同的简单的例题,以此来介绍一些构建模型的技巧.我们从中可以看到,如何选择适当的决策变量,是我们有效地建立模型的关键之一.至于对现实中错综复杂的客观问题,如何建立一个好的、适当的模型,只能有待应用者通过实践不断地去积累经验.
例1-20 (生产计划问题) 某工厂明年根据合同,每个季度末向销售公司提供产品,有关信息如表1-42所示.若当季生产的产品过多,季末有积余,则一个季度每积压一吨产品需支付存储费0.2万元.现该厂考虑明年的最佳生产方案,使该厂在完成合同的情况下,全年的生产费用最低.试建立线性规划模型.
表1-42

解 现在我们对本问题定义3种不同形式的决策变量,从而从不同的途径来构建模型.
(1)设工厂第j季度生产产品xj吨.
首先,考虑约束条件:第一季度末工厂需交货20吨,故应有x1≥20;第一季度末交货后积余(x1-20)吨;第二季度末工厂需交货20吨,故应有x1-20+x2≥20;类似地,应有x1+x2-40+x3≥30;第四季度末供货后工厂不能积压产品,故应有x1+x2+x3-70+x4=10;又考虑到工厂每个季度的生产能力,故应有0≤xj≤aj.
其次,考虑目标函数:第一季度工厂的生产费用为15.0x1,第二季度工厂的费用包括生产费用14x2及积压产品的存储费0.2(x1-20);类似地,第三季度费用为15.3x3+0.2(x1+x2-40),第四季度费用为14.8x4+0.2(x1+x2+x3-70).工厂一年的费用即为这4个季度费用之和.整理后,得下列线性规划模型:

(2)设第j季度工厂生产的产品为xj吨,第j季度初存储的产品为yj吨(显然,y1=0).
因为每季度初的存储量为上季度存储量、生产量之和与上季度的需求量之差,又考虑到第四季度末存储量为零,故有

同时,每季度的生产量不能超过生产能力:xj≤aj;而工厂4个季度的总费用由每季的生产费用与存储费用组成,于是得线性规划:

(3)设第i季度生产而用于第j季度末交货的产品数量为xij吨.根据合同要求,必须有
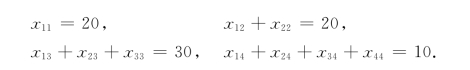
又每季度生产而用于当季和以后各季交货的产品数不可能超过该季度工厂的生产能力,故应有

第i季度生产的用于第j季度交货的每吨产品的费用cij=dj+0.2(j-i),于是,有线性规划模型:


例1-21 (多阶段投资问题) 某公司现有资金30万元可用于投资,5年内有下列方案可供采纳:
1#方案:在年初投资1元,2年后可收回1.3元;
2#方案:在年初投资1元,3年后可收回1.45元;
3#方案:仅在第1年年初有一次投资机会.每投资1元,4年后可收回1.65元;
4#方案:仅在第2年年初有一次投资机会.每投资1元,4年后可收回1.7元;
5#方案:在年初贷给其他企业,年息为10%,第二年年初可收回.
每年年初投资所得收益及贷款本金利息也可用作安排.问该公司在5年内怎样使用资金,才能在第六年年初拥有最多资金?
解 设 为i#方案在第j年年初所使用的资金数.
为i#方案在第j年年初所使用的资金数.
显然,对于3#及4#方案,仅有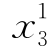 和
和 .此外,不考虑
.此外,不考虑![]() ,因为其相应投资方案回收期超过我们所讨论的期限.
,因为其相应投资方案回收期超过我们所讨论的期限.
我们将各年的决策变量(表1-43中虚线起点)及其相应效益(表1-43中虚线终点)列在表1-43内.
表1-43

显然,第j年年初可使用的资金之和应等于第j年年初所引用的决策变量之和.于是,根据表1-43所示的各种因果关系,我们不难建立如下模型:

例1-22 (混料问题) 某糖果厂用原料A,B和C按不同比率混合加工而成甲、乙、丙3种糖果(假设混合加工中不损耗原料).原料A,B,C在糖果甲、乙、丙中的含量、原料成本、加工成本、原料限量及糖果售价如表1-44所示.
问该厂对这3种糖果各生产多少千克,使得到的利润最大?
表1-44

解 设i#原料在j#糖果中的用量为xij千克.显然,j#糖果的产量为![]() .根据原料供应量情况,有约束条件
.根据原料供应量情况,有约束条件

根据各种原料在各类糖果中的含量要求,有约束条件:
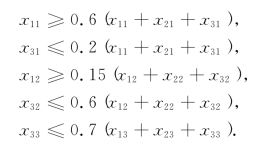
又知原料成本为

糖果加工成本为

糖果出售收入为
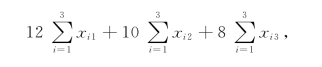
所以产品利润
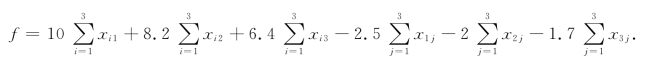
经过整理,本问题的线性规划模型为

例1-23 (人员调配问题) 某工厂车间有30个工人,每人每周工作5天,车间每天开工,每天需要的人数是波动的.周i需要人数为ai(i=1,2,3,4,5,6),周日需要人数为a7.现车间调度科希望制定一个计划,以确保休息日不连续的工人数最少,为此,准备建立一个线性规划模型.请你回答下列3个问题:(https://www.daowen.com)
(1)你准备设多少个变量?请列出;
(2)列出目标函数;
(3)在周一至周日所需人数的7个约束条件中,请列出周一所需人数18人这个约束条件.
解 (1)设xij为在第i天、第j天休息的工人数.可得下列变量:

考虑到xij与xji是同一个变量,应该删去一个,所以上述变量如果被打上*上标,这些变量就删去.我们可得到21个变量.(2)目标函数:

(3)约束条件之一:

例1-24 (场地租借问题) 某厂在今后4个月内需租用仓库堆存货物.已知各个月所需的仓库面积数如表1-45所示.又知,当租借合同期限越长时,场地租借费用享受的折扣优待越大,有关数据如表1-46所示.
表1-45

表1-46

租借仓库的合同每月初都可办理,每份合同应具体说明租借的场地面积数和租借期限.工厂在任何一个月初办理签约时,可签一份,也可同时签若干份租借场地面积数和租借期限不同的合同.为使所付的场地总租借费用最小,试建立一个线性规划模型.
解 设xij为第i个月初签订的租借期限为j个月的合同的租借面积(单位:百平方米).于是,有下列决策变量:

各个月生效的合同的租借面积为

从而,我们得如下线性规划模型:


例1-25 (多部门问题)给max{CT|AX≤b,X≥0}如下,求解该线性规划(P):

解 若取

本问题的实际背景可以如此解释:一个工厂有两个分厂,工厂统筹安排4个产品的生产,而资源b1与b2分别由分厂经营管理.
这是一个类似大系统的问题,它由若干个子系统组成.这些子系统除了有本身内部的制约关系外,各个子系统之间还有相互协调的关系,因而在反映大系统的模型中,约束条件中的矩阵A具有分块形式,其中存在若干个零矩阵.如果仍然采用单纯形法求解这种大规模线性规划问题,计算机可能发生内存不足的问题.对具有本例特点的大系统问题,已经有成熟的分解算法,我们不具体求解本例,读者可看阅相关的线性规划著作.
例1-26 (下料问题) 造纸厂接到订单,所需卷纸的宽度和长度如表1-47所示.(表中具体的单位长度是多少,我们没有给出,视具体问题而定.本教材在一些应用举例中不打算对讨论对象都给出具体的量纲而仅给出数字.例如本题在讨论时,有时连“单位长度”4个字都省去,就说宽度5,长度3 000.以后类似情况,我们不再说明.当然,在同一问题中,同一讨论对象省去的量纲单位应统一.)
表1-47

工厂生长1#(宽度10)和2#(宽度20)两种标准卷纸,其长度未加规定.现按定单要求对标准卷纸进行切割,切割后有限长度的卷纸可连接起来达到所需卷纸的长度.问如何安排切割计划以满足定单需求而使切割损失最小?
解 为了满足定单要求和使切割损失最小,我们可以使用多种切割方法来进行组合.此时,我们不但要考虑对两种标准卷纸的宽度如何进行切割,而且还要确定按某一种方式切割时标准卷纸所耗用的长度.
例如,可以把宽10的1#标准卷纸切割成宽5的卷纸2卷,根据定单要求,此时需1#标准卷纸5 000单位长度;与此同时,把宽度20的2#标准卷纸切割成宽度7和宽度9的卷纸各1卷,此时为满足定单要求,需2#标准卷纸30 000单位长度.按此切割方案,宽度9的卷纸多生产10 000单位长度,因此,切割损失的面积为(20-7-9)×30 000+9×10 000.
设xij为第i#标准卷纸按第j种方式切割时所耗用的长度.
各种可能的切割方式及切割损失宽度由表1-48给出(每种方式所产生的切割损失宽度应小于5).
表1-48

按这9种切割方式,宽度9的卷纸所得长度为
![]()
令
![]()
则宽度9、长度x1的卷纸再可切割成宽度5(切割损失宽度4)或宽度7(切割损失宽度2)的卷纸,设它们的长度分别为x2及x3.
现在切割所得宽度7的卷纸其长度为
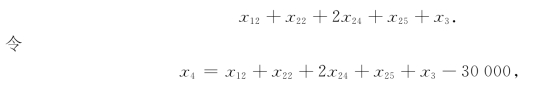
则宽度7、长度x4的卷纸又可切割成宽度5的卷纸(切割损失宽度2).
在上述切割方式组合的条件下,宽度5的卷纸其所得长度为

我们应注意到,4x2,2x3,2x4,5x5都为卷纸的切割损失面积.从而,总的切割损失面积
![]()
于是,我们得本问题的线性规划模型:
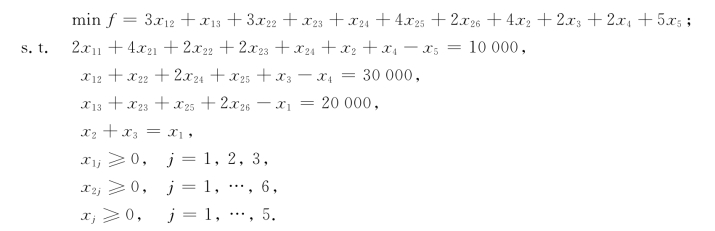
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







