若（LP）的基本可行解X的某个基本变量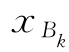＝0，则我们称X为退化的基本可行解，并称（LP）为退化的线性规划问题.

在单纯形法转轴过程中，若已选定进基本量xt，而在按最小比值准则

选择指标k时，若有两个指标k1和k2同时满足该准则，则我们可在k1和k2中任选一个作为指标k.但是在此种情况下，在转轴后的单纯形表中必然有某个基本变量为零（例如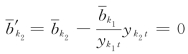，），即对应的基本可行解为退化的.

若（LP）是非退化的线性规划（所有的基本可行解非退化），那么，在用单纯形法求解的过程中，每转轴一次，由式（1－31）知，目标函数值就严格下降.这样，保证了每一个基本可行解不可能在迭代过程中出现两次.由于基本可行解的个数有限，因此，经有限步迭代后，算法一定收敛.

现在的问题是，对于退化的线性规划，是不是也能保证迭代的有限步呢？结论有两种情况：

第一种情况，对某些退化的（LP）问题，虽然在某几次迭代中，目标函数值得不到改善，使收敛速度放慢，但最终还是求到了最优解.

第二种情况，个别例子说明，单纯形法可能无穷无尽地迭代，目标函数值毫不改变.这时候，从某一个指标集IB出发经过多次转轴后又回到原来的指标集IB而产生循环，使（LP）始终达不到最优解.这种情况叫死循环.由于在实际问题中，死循环情况极少出现，因此在本书中我们不再举例作详细介绍.(www.daowen.com)

为了避免（LP）退化情况死循环的出现，在数学理论上有多种处理方法.例如，摄动法.我们介绍一种勃兰德（Bland）避免循环的方法.

1976年，勃兰德指出，在单纯形法转轴过程中按勃兰德法则来确定指标t和k，就可以避免退化问题在迭代过程中出现死循环.我们用定理1－4来给出勃兰德法则.取k＝k1，则由式（1－27）知，

定理1－4　如果在单纯形法中采用下述勃兰德法则确定指标t和k，则在迭代过程中不会出现死循环：

也就是说，按勃兰德法则，在迭代过程中如果有多个检验数rj都是负的，那么选其中下标最小的检验数的相应下标作为指标t；如果有几个同时达到

那么，选取诸Bs中最小者作为Bk.

我们完全可以根据勃兰德法则对t、k指标的选择来修改单纯形法的步骤，但是可能会使收敛的速度放慢.由于大量的实践经验表明，实际问题一般不会发生死循环情形，所以，在现代的计算机程序中没有考虑退化的问题，而仍采用一般的单纯形法.