对标准型线性规划（LP）（1－2），我们引进人工变量构造辅助规划（LP1）：

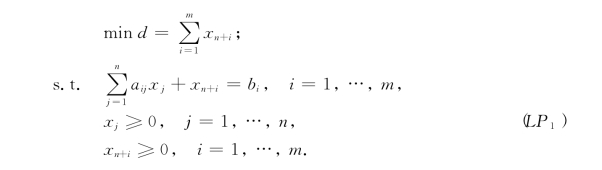
仍记XN＝（x1，…，xn）T，XM＝（xn＋1，…，xn＋m）T.

所谓两阶段法是把求解（LP）分成两个阶段：

第一阶段用单纯形法求解（LP1），根据求解结果来判别（LP）是否可行.若（LP）可行，则求得（LP）的一个初始基本可行解；

第二阶段从求得的初始基本可行解出发，用单纯形法求解（LP）.

现在我们仍假设（LP）中bi≥0（i＝1，…，m）.因此，对于（LP1）取初始指标集则XN＝0，XM＝b就是（LP1）关于基B（为单位阵I）的一个基本可行解.又因为（LP1）的目标函数d中变量的系数均为非负，故（LP1）在可行域内一定有下界，也就是说（LP1）一定有最优值.设（LP1）的基本最优解为

它们是（LP1）的m个等式约束方程

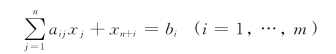
的变形.在人工变量

就得到（LP）的m个等式约束方程：

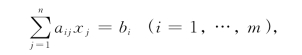
其相应的变形为

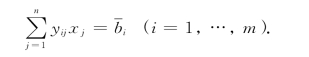
现在ykj＝0（j＝1，…，n），故上述m个方程中第k个方程就成了一个恒等式0＝0.它说明（LP）的m个方程

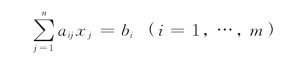
不是相互独立的，T（B＊）中第k行所相应的方程是一个多余的方程.所以，我们可以把T（B＊）的第k行元素和列元素从单纯形表中删去（对T（B＊）中r行元素按公式（1－39）、（1－40）重新计算）.

下面我们给出两阶段法的算法步骤：

①应用单纯形法求解（LP1）（取初始IB＝｛n＋1，…，n＋m｝），得基本最优解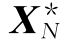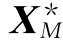，，最优基B＊，指标集IB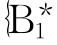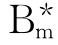＊＝｛，…，｝，单纯形表T（B＊）.

②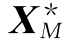＝0？

若是，则转步骤③；

若否，则（LP）不可行，算法终止.

③在IB＊中是否存在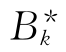＞n？

若是，则转步骤④.

若否，则转步骤⑤.

④T（B＊）中是否存在ykt≠0（t≤n）？

若是，则以ykt为枢轴元素进行转轴，得新的T（B＊），IB＊，转步骤③.

若否，则从T（B＊）中删去第k行和第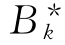列，从IB＊中删去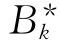，转步骤③.

⑤在T（B＊）中删除第n＋1至第n＋m列，用（LP）的目标函数系数c1，…，cn重新计算T（B＊）中r行元素，以IB＊为初始指标集，从T（B＊）出发，用单纯形法求解（LP）.

例1－16　用两阶段法求解例1－13.

解　第一阶段，引进人工变量x6和x7，得（LP1）：

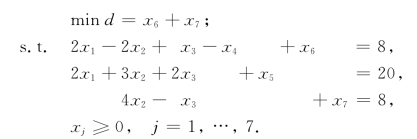
取初始IB＝｛6，5，7｝，迭代过程如表1－26、表1－27、表1－28所示.

表1－26

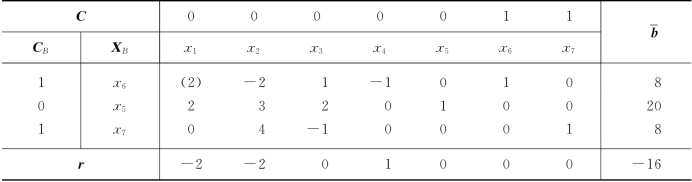
表1－27

表1－28

可知，（LP1）的最优值为0，出现情况（2）.得（LP）的一个初始基本可行解：

第二阶段，将表1－28中r行和人工变量x6及x7列删去，重新计算r行元素，得表1－29.

表1－29

由表1－29得（LP）的最优解和最优值分别为

(www.daowen.com)

例1－17　求解（LP）：

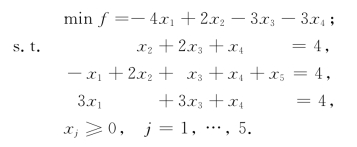
解　第一阶段，引进人工变量x6和x7，得（LP1）如下：

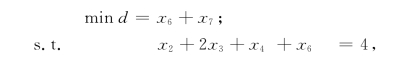
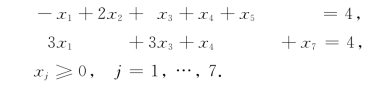
取初始IB＝｛6，5，7｝，迭代过程如表1－30、表1－31、表1－32所示.

表1－30

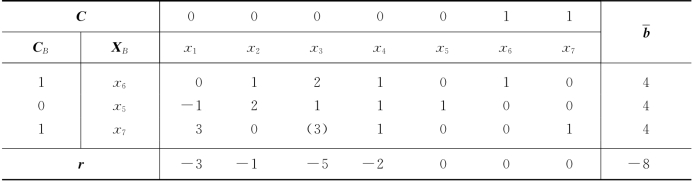
表1－31

表1－32

在表1－32中，出现了情况（3），人工变量x6为基本变量，x6＝0.我们取x6所在行的元素y11＝－1为枢轴元素进行转轴，得表1－33.

表1－33

于是，成为情况（2），得（LP）的一个初始基本可行解：

第二阶段，将表1－33中r行和人工变量x6及x7列删除，重新计算r行，得表1－34，转轴得表1－35.

表1－34

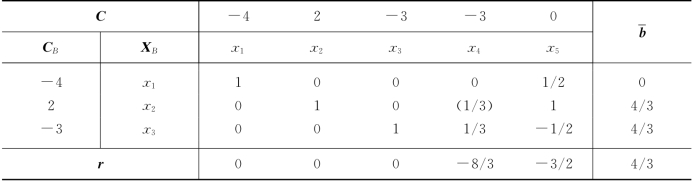
表1－35

得（LP）最优解X＊＝（0，0，0，4，0）T，最优值f＊＝－12.

例1－18　求解（LP）：

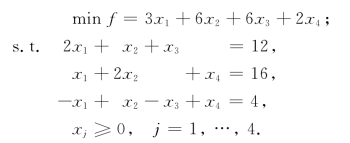
解　第一阶段，引进人工变量x5，x6和x7，得（LP1）：

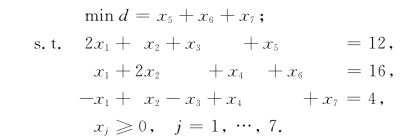
取初始IB＝｛5，6，7｝，B＝I＝B－1，迭代过程如表1－36、表1－37、表1－38所示.

表1－36

表1－37

表1－38

在表1－38中d＊＝0，人工变量x6为基本变量，x＊6＝0，x6所在行元素y21＝y22＝y23＝y24＝0，出现情况（4），因此，应从表1－38中删除第二行和x6列，重新计算r行元素，得表1－39.

表1－39

于是，成为情况（2），得（LP）一个初始基本可行解

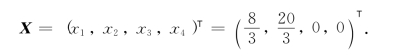
第二阶段：对表1－39，删除x5列和x7列及r行元素，重新计算r行元素，得表1－40，转轴后得表1－41.

表1－40

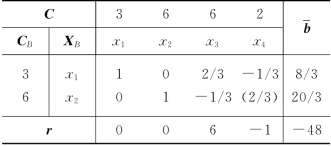
表1－41

得（LP）最优解和最优值分别为

在这里，我们指出，商规划有成功的算法，感兴趣的读者可以阅读相关的《数学规划》一类著作.