在用单纯形法求解（LP）的过程中，我们并不是对单纯形表的全部元素感兴趣的.这自然使我们想到，是否可以对单纯形法加以一定的改进，使电子计算机在实现单纯形算法时，能节省内存单元，并缩短计算时间.为此，我们对单纯形表及算法作进一步分析：

（1）作基B的单纯形表，用到矩阵B－1及

（2）确定算法是否已获得最优解，或在判定未获得最优解需确定进基变量xt的指标t，用到检验数rj（j∈ID）；

（3）确定（LP）在K内无下界，或确定出基变量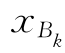的指标k，用到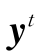及.

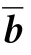（4）当已得最优解XB＝，XD＝0及最优值f0＝时，用到及f0.

故我们对T（B）中最感兴趣的元素是rj（j∈ID），yt，和f0，它们是转轴运算的必要信息.而其他元素对转轴运算不起作用.为此，我们考虑缩减单纯形表，建立改进单纯形法.其基本思想为：

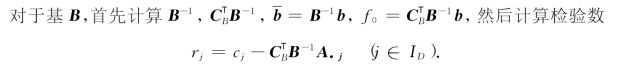
当rj≥0对j∈ID都成立时，得最优解

最优值为f0；

当rj≥0对j∈ID不全成立时，按式（1－32）确定枢轴列指标t，计算yt＝B－1A.t.由按最小比值准则（1－30）确定枢轴行指标k，得枢轴元素ykt和新基B′，视B′为新基B，重复上述步骤，继续迭代.

剩下的问题是如何求（B′）－1.我们知道，在计算机上由矩阵直接求逆矩阵，一般情况下很费时间，我们改用如下方法：

同单纯形表T（B）用枢轴元素ykt、枢轴列yt转轴一样，我们用ykt和yt对B－1进行转轴运算，来求得（B′）－1.

我们用一个实例来说明上述方法.例如，已知

其逆矩阵为

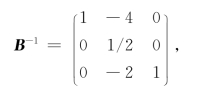
现在xt＝x1为进基变量，xB3＝x5为出基变量，yt＝（2，0，3）T，枢轴元素y31＝3.为求新基B′＝（A.4，A.2，A.1）的逆矩阵，我们对B－1进行转轴运算：

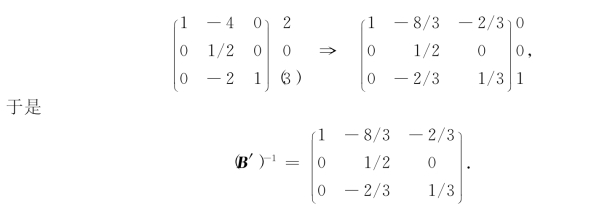(www.daowen.com)

得k＝3，枢轴元素y34＝1.

我们把上述运算列成表1－16.

表1－16

第二步，进行转轴运算：

定指标t、计算yt；定指标k，得表1－17.

表1－17

继续迭代，得最优表如表1－18.

表1－18

由表1－18得本问题的最优解和最优值分别为

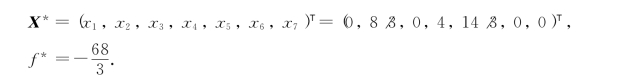
当（LP）中变量个数n大大超过约束方程的个数m时，在电子计算机上使用改进单纯形法，可以节省较多的内存单元和减少计算量.同时，为了避免舍入误差的积累，当计算机求解（LP）迭代了一定的步骤后，可重新由（LP）的原始数据B，CB和b直接计算，以校正当前的矩阵G，保持算法的稳定性.这里我们顺便指出，在用手工计算时，使用改进单纯形法并没有减少计算量.