在§1.2线性规划的几何特征这一节中，我们曾经指出，若线性规划存在最优解，则可分为最优解唯一和不唯一.那么，在用单纯形算法求解所得的最优单纯形表中（基本最优解对应的单纯形表今后称为最优单纯形表，简称最优表，相应的基称为最优基），如何反映这种情况呢？让我们来看两个例子.

例1－9　给出下列线性规划的全部基本最优解：

解　用单纯形法求解本问题，得最优单纯形表如表1－10.

表1－10

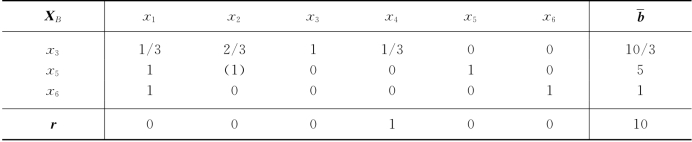
在表1－10中，非基本变量x2的检验数r2＝0，而y12＞0，y22＞0，所以最小比值准则有效.我们选x2为进基变量、x5为出基变量，转轴后得到另一张最优表表1－11.

表1－11

类似地，我们还可以得最优表如表1－12和表1－13.

表1－12

表1－13

由表1－10至表1－13，我们得到本问题的4个基本最优解：

它们的目标函数值都是同一个值f＊＝－10.

进一步地，我们还可以给出最优解的一般表达式：

例1－10　对下列线性规划的最优解进行讨论：

解　用单纯形法求解本问题，可得最优单纯形表如表1－14.(www.daowen.com)

表1－14

我们得基本最优解X＊＝（30，20，0，0，0，）T，最优值为－40.

现在在表1－14中非基本变量的检验数r3＝0，且y13＝－2＜0，y23＝－7＜0，最小比值准则失效，但我们若取

于是，由式（1－34）可知，

且相应可行解

的目标函数值也为－40，所以也为最优解.

类似地，由于表1－14中非基本变量x4的检验数r4＝0，且y14＝－1＜0，y24＝－2＜0，可知

也为本问题的最优解.

通过例1－9和例1－10的讨论，我们有如下结论：

若用单纯形法求解（LP）得最优单纯形表T（B＊），相应的最优基为B＊，则

（1）若T（B＊）中非基本变量的检验数全大于零，则（LP）有唯一基本最优解；

（2）若最优表T（B＊）中存在t∈ID，rt＝0，且yt＝（y1t，…，ymt）T中存在大于零的元素，则按最小比值准则（1－30）选定出基变量，转轴后可得（LP）的另一个基本最优解；

（3）若最优表T（B＊）中存在t∈ID，rt＝0，且yit≤0（i＝1，…，m），则按式（1－33）和式（1－34）所取的可行解

也为最优解.