若初始指标集IB对应的单纯形表T（B）中存在某个rj＜0（j∈ID），我们就从这个基本可行解X0出发，寻求另一个基本可行解X′，使CTX′＜CTX0.从几何意义来说，也就是寻找顶点X0的相邻顶点X′.

根据相邻顶点的定义，新的指标集

仅有一个指标不同，不妨设第k个指标不同：

也即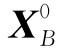中的一个基本变量xBk在新的基本可行解X′中成为非基本变量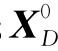；中的一个非基本变量，例如xt，在新的基本可行解X′中成为基本变量.这种从X0及T（B）出发，寻求X′及T（B′）的运算过程，我们称它为“转轴”或“转基”，并称xt为进基变量，xBk为出基变量.

现在我们要解决的一系列问题是：换出指标Bk、换进指标t怎样选取能使B′成为基？在什么条件下IB′对应的基本解X′是可行解，并使f（X′）不大于f（X0）？如何由T（B）得到新的T（B′）？这些问题都必须在转轴过程中给以完美的解决.

如果由IB′仍能产生一个基本解（｜B′｜≠0），那么，对IB′来说，应能从（LP）关于基B的典型方程组：

用消元法得到关于基B′的典型方程组：

设ykt≠0（保证B′也为基），将方程（1－20）两端除以ykt，可得方程（1－24）；将方程（1－19）减去方程（1－24）乘以yit，可得方程（1－23），将方程（1－21）减去方程（1－24）乘以rt，可得方程（1－25）：

显然，它就是我们所需要的（LP）关于基B′的典型方程组，将它与方程组（1－22）作比较，可得如下公式：

于是，根据这些公式，就可以由T（B）来确定T（B′）.如前所说，此运算过程称为转轴，因而，上述公式称为转轴公式.T（B）的第t列（相应于xt的列）称为枢轴列，第k行（相应于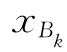的行）称为枢轴行，ykt称为枢轴元素.

可见，如果IB能对应一个基本解，则IB′也能对应一个基本解的充分必要条件为ykt≠0.

下面我们来讨论指标k的选取.

在转轴过程中，我们应保持IB′对应的基本解X′的可行性，也即要求T（B′）中（i＝1，…，m）成立.由式（1－27）可知

因此，当指标t确定后，应依据下述准则（称为最小比值准则）来确定指标k：

接下来，我们考虑指标t的选取.(www.daowen.com)

由式（1－29）知：

这就是确定指标t的准则.一般地，我们取

我们将上述的讨论归结为下列定理.

定理1－2　设B为（LP）的一个基，相应的指标集

X为关于B的基本解，在单纯形表T（B）中有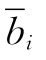≥0（i＝1，…，m），则

（1）若T（B）中各检验数rj≥0（j＝1，…，n），则X必为（LP）的一个基本最优解；

（2）若存在检验数rt＜0（t∈ID），且存在yit＞0（1≤i≤m），按最小比值准则（1－30）确定指标k，按式（1－17）确定指标集IB′，则单纯形表T（B′）中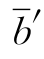≥0（i＝1，…，m）一定成立，且T（B′）中的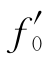必不超过T（B）中的f0，特别地，当T（B）中的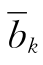＞0时，必有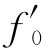＜f0；

（3）如果T（B）中存在rt＜0（t∈ID），且对i＝1，…，m，均有yit≤0，则（LP）的目标函数值f在可行域中无下界.

证　（1）与（2）前面已作了说明，现证（3）.

我们按下列方法在K中取可行解.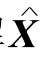

设j∈ID，令

其中ε为任一正数.从而，由方程组（1－13）和式（1－14），可知

因为yit≤0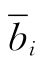，≥0（i＝1，…，m），ε＞0，所以≥0（i＝1，…，m）.从而，由此取得的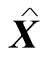是（LP）的一个可行解.

因为rt＜0，故当ε→＋∞时，f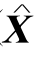（）→－∞，所以（LP）的目标函数值在K中无下界.