若取初始指标集IB＝｛B1，…，Bi，…，Bm｝，相应矩阵B（｜B｜≠0）为基，基本解X0可行.对下列m＋1个方程

用消元法将其化成下列关于基B的典型方程组：

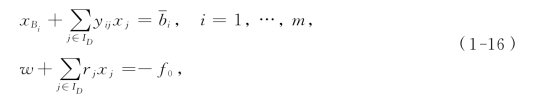
我们把这m＋1个方程的有关信息制成表1－3，称它为（LP）关于基B的单纯形表，记为T（B）.（变量w在m＋1个方程中的有关系数未在T（B）中列出，在本书中，凡出现符号T（B），都是指关于基B的单纯形表.）

表1－3

由T（B）可知，关于基B的基本可行解X0为

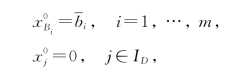
其目标函数值f（X0）＝f0.(www.daowen.com)

在表1－3中，基本变量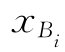对应的方程

处在表的第i行，这就是Bi下标i的具体意义，而Bi是｛1，…，n｝中某一个数字.一串数字为了表达某种排列顺序，数学中常用此种描述方式，请读者深刻理解.

由方程（1－14）知，对任可行解X∈K，有

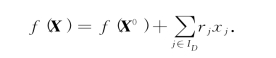
因为可行解X的非基本变量xj≥0（j∈ID），所以，当单纯形表T（B）对任j∈ID都有rj≥0时，则基本可行解X0对应的目标函数值f0＝f（X0）不大于（LP）任一可行解X的目标函数值f（X），于是X0即为（LP）的基本最优解，f（X0）＝f0即为（LP）的最优值.

在单纯形表中，我们称rj（j＝1，…，n）为检验数.

称各检验数rj≥0（j＝1，…，n）是基本可行解X0为最优解的最优性条件.

请读者注意，在部分运筹学著作里，把目标函数求max作为线性规划的标准模型，那么，基本可行解为最优解的最优性条件变化为：在单纯形表中所有的检验数rj≤0.