现在我们引进有关的代数知识来阐述顶点.

假设标准型线性规划（1－2）或（1－3）的m个等式约束方程：

是相互独立的.现在从n个变量x1，…，xn中选取m个变量xB1，…，xBm（变量x的下标B1，…，Bi，…，Bm为｛1，…，n｝中数字，B1，…，Bi，…，Bm为m个数字的某种排序），它们在（LP）（1－3）的系数矩阵A中相应的系数列向量，…，构成矩阵

我们称变量xB1，…，xBm为（LP）关于基B的基本变量，变量xj（j∈ID）为（LP）关于基B的非基本变量.

若对j∈ID，取xj＝0，代入方程组AX＝b，可得方程组

由于｜B｜≠0，此方程组能唯一地确定变量xB1，…，xBm的值.设方程组BXB＝b的解为

为AX＝b的一个解.我们称

为（LP）关于基B的一个基本解.如果基本解又满足非负条件，即有≥0（i＝1，…，m），则称它为（LP）关于基B的一个基本可行解.

如果将上一节所述的独立变量与非独立变量，与本节引进的非基本变量与基本变量相对应，我们可以发现，（LP）的基本可行解就是（LP）可行域K的顶点.我们将前面对（LP）几何特征讨论分析所得结论归纳成下列基本定理.

定理1－1　（基本定理）　对于标准型线性规划（LP）：

（1）若（LP）有可行解，则（LP）必有基本可行解；(www.daowen.com)

（2）若（LP）有最优解存在，则（LP）必有基本最优解（既是基本解又是最优解）.

联系我们在分析标准型线性规划（LP）几何特征时对相邻顶点的解释，可知，若是两个基本可行解的非基本变量指标集仅有一个指标不同（即基本变量指标集仅有一个指标不同），那么，从几何意义上来说，这两个基本可行解就是相邻的顶点.

下面我们来讨论如何方便地求得（LP）的基本解和其目标函数值.

如果我们把（LP）的目标函数f也看成一个变量，并令w＝－f，则f＝c1x1＋…＋cnxn变换成

当（LP）的指标集IB（｜B｜≠0）和ID给定后，我们对（m＋1）个方程

用消元法作等价变换，化成下列形式：

其中j∈ID（这里，yij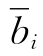，，rj，f0是上述方程组中系数的记号）.此方程组的特点为：基本变量xBi仅在第i个方程出现且系数为1，而在其他m个方程中均不出现；w仅在最后一个方程出现且系数为1，而在其余方程均不出现.我们称该方程组（1－12）为（LP）关于基B的典型方程组，它对我们讨论问题会带来许多方便.因为方程组（1－12）即为下列形式：

一旦n－m个非基本变量xj（j∈ID）的值取定，则基本变量xB1，…，xBm的值也就取定，相应地，X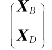＝的目标函数值f（X）同时也被确定.所以方程组（1－13）和方程（1－14）就是用非基本变量xj（j∈ID）来表示基本变量xBi（i＝1，…，m）和目标函数值f（X）.

特别地，取xj＝0（j∈ID），即得xBi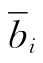＝（i＝1，…，m）.换言之，我们由方程组（1－13）和方程（1－14），可得基本解X0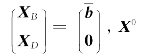＝的目标函数值f（X0）＝f0.