对标准型线性规划（LP）解的几何特征，我们不打算进行详细的数学论述，而仅仅用类比法，给出如下结论：

（1）如果可行域K≠∅，则K必是Rn的第一卦限中的一个凸集，K的顶点一定存在.

（2）如果最优解X＊存在，则最优解中至少有一个为K的一个顶点.这就给我们求解（LP）指出了一个方向：我们不必在凸集K（如果不是空集）的内部搜索（LP）的最优解，而只要对K的顶点相应的目标函数值进行比较，就一定能在K的顶点中找到最优解（如果最优解存在）.因此，K的顶点将是我们关心和研究的对象.下面我们来讨论如何用代数方法确定K的顶点.

由图1－1知，例1－4所给两个变量的线性规划问题（1－6）的5个顶点（x1，x2）T为

现在我们将问题（1－6）标准化：

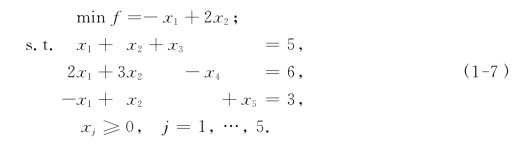
该模型的可行域K为R5中第一卦限内的凸集.我们将上述5个点的坐标代入方程组：

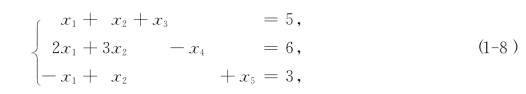
即可解得x3，x4和x5.于是，K在R5中相应的顶点为(www.daowen.com)

我们可以发现，这5个点都有两个变量取值为零.

那么，如果没有图1－1，我们应如何确定问题（1－7）可行域的顶点的坐标呢？这个问题是不难解决的.问题（1－7）有n＝5个变量、m＝3个等式约束，我们可在5个变量中，任取n－m＝5－3＝2个变量为独立变量，并让它们取值为零，代入等式约束方程组（1－8），解出另外3个非独立变量的值，这样，我们可得下列10组解：

其中5个解就是我们上面所说的可行域K的顶点；另外5个解没有满足变量都应取非负值的约束条件，不是可行解，当然不可能是K的顶点.

推而广之，对于具有n个变量、m个独立等式约束方程的（LP）来说，它的可行域K的顶点可用如下方法来确定：

在n个变量中选取n－m个变量为独立变量（在下一节，被称为非基本变量），并对它们取值为零，再将它们代入等式约束方程组，若能唯一地求得另外m个非独立变量（在下一节，被称为基本变量）的值，而且此m个变量的值均为非负数，则这n个变量的值就是K的一个顶点的坐标.

下面我们给出相邻顶点的概念.由图1－1可知，顶点X1＝（1，4）T与顶点X2＝（5，0）T是R2中K的两个相邻的顶点，对于问题（1－7）来说，它们相应地成为X1＝（1，4，0，8，0）T与X2＝（5，0，0，4，8）T.X1是把x3和x5视为独立变量并取值为零而得到的，X2是把x2和x3视为独立变量并取值为零而得到的.可见，对这两个相邻顶点来说，取值为零的独立变量（即非基本变量）仅有一个不相同.类似地，在Rn空间中，（LP）的可行域K的两个相邻顶点各自相应的n－m个独立变量（取值为零）之间，也仅有一个不相同.