让我们先来讨论两个变量的线性规划问题的可行域K及最优解的几何特征，对其最优解可能出现的各类情况作一个几何直观的认识.

例1－4　求解线性规划：

解　因为该线性规划仅有两个变量，我们在x1Ox2坐标平面内用图解法来求解此问题.

第一步，确定可行域K.

不等式x1≥0表示以x2轴（直线x1＝0）为界的右半平面，不等式x2≥0表示以x1轴（直线x2＝0）为界的上半平面，所以该线性规划的可行解X＝（x1，x2）T必在第一象限.

x1＋x2＝5是一条直线（选取两个点（0，5）T及（5，0）T连成直线即是），它把x1Ox2坐标平面分成两个半平面.为确定哪一个半平面是符合约束条件x1＋x2≤5的，我们只要把原点（0，0）T代入不等式x1＋x2≤5中：若不等式成立，则我们就取原点所在的那一个半平面（以x1＋x2＝5为界）表示x1＋x2≤5，否则就取不含原点的那个半平面.我们在直线的两端画垂直箭头指向符合约束条件的半平面.

同样，2x1＋3x2≥6和－x1＋x3≤3各对应着一个半平面.

所以，可行域K为上述5个半平面之交集，它是一个在第一象限的凸多边形（包括边界），如图1－1中的阴影线部分所示.

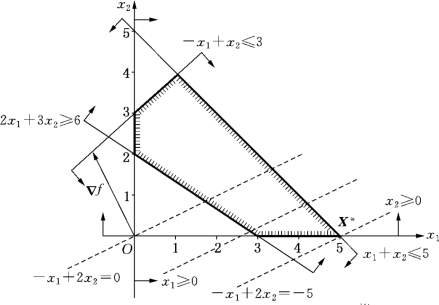
图1－1

第二步，寻找最优解.

我们结合目标函数f＝－x1＋2x2＝c1x1＋c2x2来求线性规划的最优解.对于任一给定的实数α，方程

为一条直线.由于位于该直线上的点都具有相同的目标函数值α，故而称它为等值线.当α的数值变动时，我们就得到一族相互平行的直线，它们的斜率都为－.我们知道，目标函数f作为x1及x2的函数，它在任一点的梯度都是

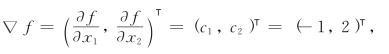
它与目标函数的等值线垂直.由高等数学有关知识可知，当点（x1，x2）T沿梯度方向移动时，f的值将随之增大；沿着负梯度方向移动时，f的值将随之减少.不妨在原点作梯度C＝（c1，c2）T＝（－1，2）T（从原点至点（c1，c2）T作一向量即为原点的梯度），过原点作向量C的垂直线（用虚线表示），它为过原点且α＝0的等值线

因为我们的问题是求min f，因此让等值线逆梯度方向移动，使c1x1＋c2x2＝α的值α逐步减小.当它刚要离开K（此时，与K仅有一个交点X＊＝（5，0）T）时的等值线

(www.daowen.com)

对可行域K内各点的f值来说，其值α＝f＊＝f（X＊）＝－5最小.所以，顶点X＊＝（5，0）T即为线性规划（1－6）的最优解，f＊＝－5即为最优值.

倘若我们将例1－4的目标函数改为求max，则我们将等值线沿梯度方向移动，此时c1x1＋c2x2＝α的值逐步增加，当它刚要离开K时的直线－x1＋2x2＝7（与K的唯一交点X＊＊为（1，4）T），对可行域K内各点的f值来说，其值α＝f＊＊＝f（X＊＊）＝7最大，因此，K的顶点X＊＊＝（1，4）T为最优解，最优值f＊＊＝7.

例1－4从几何直观上告诉我们，若两个变量的线性规划问题的最优解存在且唯一，则最优解必为可行域K的一个顶点，而K为凸多边形.

对于目标函数求min的两个变量的线性规划，根据目标函数的等值线与可行域K的各种关系，我们可以得知它的解可能会出现以下几种情况.

（1）最优解存在且唯一.这时，K是一个非空的、有界或无界的凸多边形，最优解X＊必为K的一个顶点，最优值f＊为一个有限值，如图1－2所示.

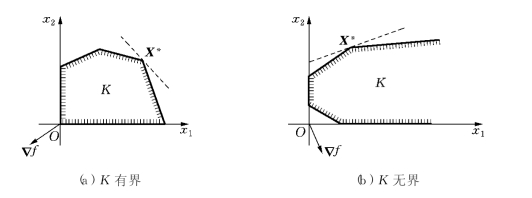
图1－2

（2）最优解X＊存在但不唯一.这时，K是一个非空、有界或无界的凸多边形，最优值f＊是一个有限值.f的等值线c1x1＋c2x2＝f＊与K之交是K的一个边界，因此该边界上的点都为最优解；但是，我们至少可以取到K的一个顶点为最优解，如图1－3所示.

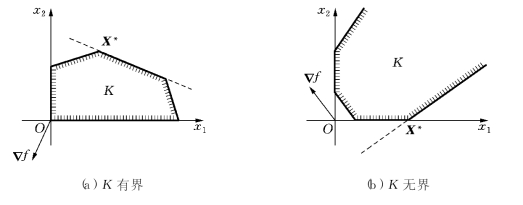
图1－3

（3）可行解存在但目标函数值在K内无下界（简称线性规划无下界）.这时，K必是一个非空无界的凸多边形，最优解不存在，min f→－∞，如图1－4所示.

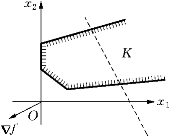
图1－4

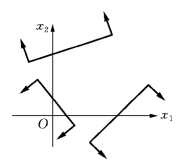
图1－5

（4）可行解不存在（或称线性规划不可行）.这时，K为空集，如图1－5所示.

通过以上各种情况的分析，关于2个变量的线性规划的解，我们可以得到以下两点结论：

①如果K≠∅（空集），则K必是x1Ox2坐标平面第一象限内的一个凸多边形（今后，在线性规划理论中，称为凸集），K的顶点一定存在.

②如果最优解X＊存在，则最优解中至少有一个为K的顶点.