由于求解数学模型的算法都是为标准化的模型设计的，所以，为了便于对求解线性规划模型建立一个有效的算法，我们有必要对线性规划模型规定它的标准形式.今后，我们谈到的线性规划模型的标准型，都是指下列形式：

也就是说，线性规划的标准型，是指：对目标函数一律求最小值；决策变量一律为非负变量；约束条件除变量的非负条件外一律为等式约束.今后，记线性规划模型的标准型为（LP）.

若令

则（LP）便可写成下列形式：

式（1－3）、式（1－4）中的X≥0均表示X中的各个分量xi≥0（今后此类符号意义与此相同，不再说明）.对于（LP），其可行域K我们常写成：

各种形式的线性规划模型都可以化成标准型：

（1）若线性规划为

这时，只需要将求目标函数的最大值变换为求另一个目标函数的最小值：

令f＝－z，于是，得到（LP）：

（LP）与原有问题具有同样的可行域和最优解（若存在），只是最优值（若存在）相差一个符号而已.求解原有问题转化成求解（LP）.

（2）约束条件为不等式.

如果线性规划具有不等式约束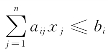，这时我们可引进一个新变量x′，用下面两个约束条件代替这个不等式约束：

我们称x′为松弛变量.(www.daowen.com)

如果线性规划具有不等式约束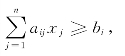

这时我们引进一个新变量x″，并用下面两个约束条件代替这个不等式约束：

我们称x″为剩余变量.

有时，x′和x″统称为松弛变量，它们在目标函数中的系数都为零.

（3）决策变量xj为自由变量：xj≷0.

解　它共有4处不符合标准型要求：对目标函数z是求最大值；x2≤0；x3为自由变量；第一、第二、第三个约束条件为不等式.为此，我们通过以下步骤把该模型标准化：

（1）令f＝－z，把求max z改变为求min f；

（2）用－x4替换x2，x4为非负变量；

（3）用x5－x6替换x3，其中x5≥0，x6≥0；

（4）对不等式约束分别引进松弛变量x7和剩余变量x8，x9.

于是，得本问题的标准型：