在经济建设、企业管理和生产实践的各项活动中，我们常常面临把有限的资源分配到若干活动上去的分配问题：

（1）对有限的资金、材料、设备、场地、能源和劳动力等财力、物力和人力，如何以最佳方式作有效的分配，以期望获得最大的效益.

（2）在既定的任务之下，如何统筹安排，以做到用最少量的财力、物力和人力来完成任务.

这些最优分配问题的数学模型在运筹学中处于中心的地位，而线性规划是解决这一类问题的一个理论和方法都比较成熟的运筹学分支.下面我们来看两个实例.

例1－1　（生产计划问题）　某工厂生产1＃，2＃和3＃三种产品，每种产品需经过3道工序.每件产品在每道工序中的工时定额、每道工序在每周可利用的有效工时和每件产品的利润由表1－1给出.问每种产品各生产多少，可使这一周内生产的产品所获利润最大？

表1－1

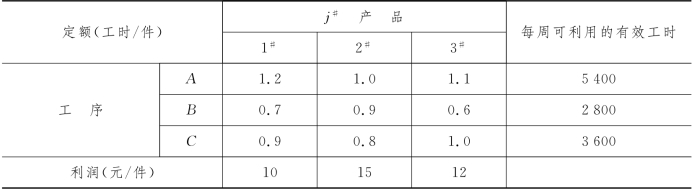
解　本问题是要把有限的工时资源合理地分配到3种产品的生产活动上去，以期望获得最多的利润.

首先我们引进决策变量：设一周内j＃产品的生产件数为xj（j＝1，2，3）.

然后，根据每件产品的工时定额以及各工序允许的有效工时列出约束条件：

1＃产品每生产一件需A工序1.2工时，现生产x1件，故1＃产品耗费A工序的工时数为1.2x1.类似地，生产2＃产品和3＃产品耗费A工序的工时数分别为1.0x2和1.1x3，所以3种产品对A工序的工时总需求量为

它不应超过A工序在一周内所允许的工作时间5 400工时.于是，得工序A加工产品的约束条件：

类似地，对工序B和C有以下约束条件：

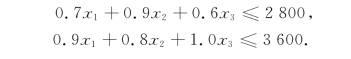
再者，变量x1，x2和x3只能取非负值，故有下列非负约束条件：

最后，我们来确定产品生产的效益.若用f表示工厂一周内生产3种产品所能获得的利润，则有

现在工厂的目标是希望获得最大利润，我们写成：

综上所述，我们得本问题的数学模型：

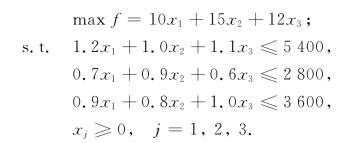
其中，s.t.为英文“subject to”（受约束于）的缩写.

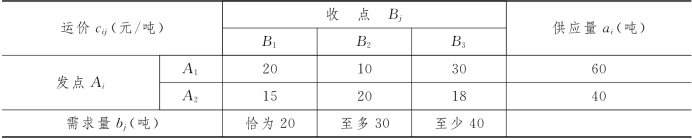
例1－2　（运输问题）　两个发点A1和A2有物资必须运往3个收点B1，B2和B3.发点Ai对物资的供应量ai、收点Bj对物资的需求情况和发点Ai至收点Bj每输送一吨物资所需的运输费用cij见表1－2.为完成发点A1和A2对物资的运输任务，问运输方案应如何确定，而使总运费最少？

表1－2

(www.daowen.com)

解　本问题是在完成既定运输任务的条件下而希求花费最少的财力.

设xij为从发点Ai运送到收点Bj的物资数量.

由于发点Ai的ai吨物资必须运走，因此，ai等于发点Ai运往各收点Bj的运量xij之和.由此得约束条件：

注意到各收点Bj对物资的需求情况，我们有下列约束条件：

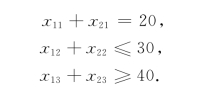
自然，运量xij都应为非负变量：

总运费为

我们对f求最小值.故本问题归结为如下数学模型：

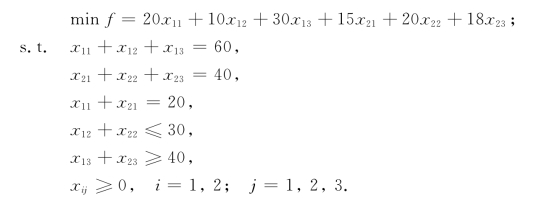
上述建立的两个数学模型，我们称之为线性规划.可见，线性规划模型具有下列3个要素：

（1）决策变量.这些决策变量的一组定值代表所给问题的一个具体方案.一般来说，这些决策变量都是非负变量.如果在模型中变量xj的符号不受限制，即变量xj取正值，取负值或取零都可以，我们把它写成条件xj≷0，并称xj为自由变量.

（2）约束条件.这些约束条件都为线性等式或线性不等式，它们反映了所给问题对资源的客观限制及对所要完成的任务的各类要求.同时，对决策变量的符号要求也属于约束条件.

（3）目标函数.它为决策变量的线性函数.按所给问题的不同，可要求目标函数f实现最大值或最小值.

为此，线性规划模型的一般形式为

其中符号≷表示≥，＝，≤这3个符号中的任意一个.

我们给出线性规划的有关术语：

可行解——满足线性规划全部约束条件的解X＝（x1，…，xn）T称为线性规划的可行解.

可行域——全体可行解的集合称为线性规划的可行域.用符号K表示.

最优解——使目标函数实现最小值（或最大值）的可行解X＊＝（x1，…，xn）T称为线性规划的最优解.

最优值——最优解的目标函数值

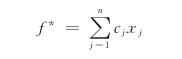
称为线性规划的最优值.