我们应该看到，当时西学传播的程度受制于解读者和受众的知识基础。《重学》极大部分介绍的是19世纪以前的初等力学知识^[82]，即便如此，它也是近代物理科学数学化的结果，有着必要和必需的数学基础。

惠威尔的《初等力学教程》第5 版涉及的数学基础知识主要有：算术、三角函数、平面几何、单变量函数微分^[83]、圆锥曲线（主要是抛物线）。这当中最深的就是圆锥曲线。在《重学》初版时（1859年）的中国，《代微积拾级》刚刊行，《圆锥曲线说》还未译出。抛射运动涉及的抛物线知识对国人来说几乎是全新的知识，所以也难怪之后大部分数学家都是尽量抛开抛物线谈抛射运动，对于《重学》卷11 的第5 款和第6 款（子弹轨迹为抛物线的证明）并不理会。李善兰巧妙地用“平圆”解读，随后的华蘅芳改用四率比例算法进行解读，之后的数学家大都如此。可以说，抛射运动知识因《重学》的翻译而传入中国，因《火器真诀》的解读而为一般中算家所掌握，因中算家的再解读才逐渐被炮兵们所理解。

实际上，从力学发展历史来看，它同数学的发展是同步的。伽利略、惠更斯、莱布尼茨的时代，力学研究的主要内容是自由质点的运动，特别是解决在引力作用下的自由质点的运动。哲学家和科学家都力图用力学语言来描述自然界的运动，并以力学理论为基础来对物体的运动和变化作出解释。在几何方面的主要工具是解析几何，特别是有关圆锥曲线的解析几何，它能把物体的形状和运行路线表示为代数形式，从而导出数量关系。这是产生加速度和万有引力概念的必要的工具。伽利略从自由落体运动规律中归纳出加速度的概念时，用到了抛物线的性质。牛顿从行星运动规律中导出了万有引力定律，需要用椭圆的性质。在计算方面则是引进了变量，发明了微积分。^[84]

数学关系是宇宙之钥，万物通过数学得以理解；把基本的物理原理表示为定量的数学陈述，然后利用数学的论证推导出新的物理成果。这种由伽利略开创并由牛顿继承的工作方法由他们的后来者继续向前推进。力学被看成是一种公理化系统，当成数学的一个分支，力学问题可以用数学方法定量地解出。18世纪的力学表现出分析化，如建立了与牛顿力学三大定律并行的其他一般性原理，普遍原理、定律公式化；引入广义的坐标系统，将力学问题代数化。拉格朗日曾在其《分析力学》（1788年）中说：“我曾致力于将这门科学（力学），以及解决与它有关的问题的技巧，化归为一般性的公式，这些公式的简单推导就给出解决每一个问题所必需的全部方程……在这项工作中找不到图形。我在其中所阐明的方法，既不要求作图，也不要几何的或力学的推理，而只是一些遵照一致而正规的程序的代数（分析）运算。喜欢分析的人将高兴地看到力学变为它的一个新分支，并将感激我扩大了它的领域。”他的一个重要工作就是选出达朗贝尔原理和最小作用原理作为整个力学的最基本原理，用分析的工具将经典力学重建，使得力学成为当时最为完备的一门自然科学学科。数学是探究、发现和描述物理现象的最佳方法，它被分成两部分，一部分是由纯粹的抽象的东西组成，另一部分是由物理-数学的混合物组成（混合数学，mix mathematics），包括那些能用数学方法进行研究和处理的领域，包括力学、光学、天文学、军用和民用建筑、保险业、声学和音乐。^[85]因此，要理解和吸收当时的科学成就，必须具备必要的甚至是充分的数学知识才行。

力学与数学的关系，晚清国人也有一定的认识。王韬在《重学浅说》中就有所论述，他说：

重学莫精于英人胡威立，其理根于算学兼通格致，不惟有用于制器并有裨于考天。言物之测算则为度量之学，言物之轻重则为权衡之学。盖几何者，度量之学也；重学者，权衡之学也。昔西人以权衡之学制器，以度量之学考天；今则制器、考天皆用重学。重学中有推算一法，知无论何器能增力者，不能增速，能增速者必费大力，至机件运动一切皆有法。凡机器之繁，均藉六类简器并合而成。重学实用，为造机器、汽机各书无一不从重学中来尔。迩来轮船、火车、工艺、制造、各厂工程之钜者，悉由此出。重学讵不为格致之要学也哉。^[86]

钱熙辅在《重学》跋文中说：

其动重学有平速、加速之分，而地心下引之力为渐加速。速之比例用股而不用弦，故物自上而下，弧线长于圆径，圆径长于通弦，而其时刻无不同者，此皆理势之自然。

按《重学》第十卷第三款（命题）“设平圆之直交地平，自顶点至圆界作诸通弦，则物任于通弦下行自顶点至末点时刻俱等”，书中有详细的数理推导过程。显然，钱氏跋文中“理势之自然”的认识是针对此而言。

1883年，丁韪良在同文馆讲授《格物测算》课程，该书是丁氏自编教材，“皆用算学诸理，以推物力，意在用算而不在讲算也，除几何、形学、勾股、代数常用外，其微分积分亦恒有不得已而借用者”^[87]。此书多次引用《代微积拾级》中的定理作为已知理论，涉及求微分、求积分、求多重微分及利用微积分求曲线长度、曲面面积、旋转体体积等知识内容，书中直接应用公式。这说明学生当时要具备相当的数学知识基础。

类似的，另外两部李善兰参与翻译的经典著作《谈天》和《数理格致》在晚清的传播都要面对同样的问题——晚清中国人并不具备理解它们的必要的或充分的数学基础。(www.daowen.com)

李善兰在《谈天》序中，在对哥白尼日心说简介之后有一番告诫，他说：

……刻白尔（即开普勒）求其故，则知五星与月之道皆为椭圆，其行法面积与时恒有比例也。然俱仅知其当然，而未知其所以然。奈端（即牛顿）求其故，则以为皆重学之理也。凡二球环行空中，则必共绕其重心，……故绕重心即绕日也。凡物直行空中，有他力旁加之，则物即绕力之心而行。而物直行之迟速与旁力之大小，适合平圆率，则绕行之道为平圆；稍不合，则恒为椭圆。惟历时等，所过面积亦等，与平圆同也。今地与五星本直行空中，日之摄力加之，其行力不能适合平圆，故皆行椭圆也。由是定论如山不可移矣。又证以距日立方与周时平方之比例及恒星光行差、地道半径视差，而地之绕日益信。证以煤坑之坠石，而地之自转益信。证之彗星之轨道、双星之相绕，多合椭圆，而地与五星及日之行椭圆益信。余与伟烈君所译《谈天》一书，皆主地动及椭圆立说，此二者之故不明，则此书不能读，故先详论之。^[88]

这种“有言在先”的告诫，一方面是因为地动说与之前流行的“地静说”相矛盾，另一方面也是因为《谈天》中涉及很多有关椭圆运动的数学知识（这段涉及开普勒行星运动的三大定律），需要事先给读者提个醒。我们看看《谈天》中的一些图示（图5-3-3）就可以感知其中的数学知识并不简单，要达到“知其所以然”并非易事。所以梁启超在《读西学书法》中称：“《谈天》一书，必通算学，明测算，乃能卒业。”^[89]

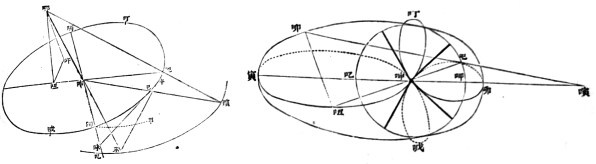
图5-3-3　《谈天》卷十二《摄动》和卷十四《逐时经纬度之差》中的原图

按韩琦先生的研究，李善兰和伟烈亚力大约在1859年前后试图翻译牛顿的《自然哲学的数学原理》一书，但并没有完成，只是翻译了其中的定义、运动的公理和定理，以及第一编“物体的运动”的前四章，此即未完成的《数理格致》。^[90]在17世纪的英国，《自然哲学的数学原理》发表后，许多读者根本读不懂，以至于当时有人认为牛顿写了一本连他自己也看不懂的书，书中令人眼花缭乱的数学技巧使许多同时代的一流数学家也感到非常吃力。^[91]这对于连《重学》中几款涉及抛物线知识的定理都需要借助于“平圆通之”的晚清国人来说，阅读难度自然可想而知，更何况是翻译了！丁福保曾记述《数理格致》说：

是书分平圆、椭圆、抛物线、双曲线各类，椭圆以下尚未译出。其已译者，亦未加删润，往往有四五十字为一句者，理既奥赜，文又难读。吾师若汀先生屡欲删改，卒无从下手，后为大同书局借去，今已不可究诘。^[92]

缺乏相应的数学基础应该是《数理格致》不能在晚清流传的主要原因，这恐怕也是两位译者未能全部完成翻译的重要原因之一。^[93]

因此，我们应该看到，晚清西学传播必须面对的三个情形。首先，西学知识并非由浅入深依次传入；其次，有着自己算学传统的中算家并不具有完备的解读西学的知识构成，而受众群体的知识基础更为薄弱；最后，很重要的一点，当时特定的“算学-自强”的社会因素要求某些西学必须引入并且尽可能地为受众所掌握。鉴于此，对照前文的分析可以看出，中算家们实际上是在根据自己和受众的知识构成对西学加以选择、解读和建构，赋予西学在自己知识结构内以意义，这同时也是他们不断修正、扩充自己的知识构成的过程。因此，差不多半个世纪之后的邓钧能直接运用“抛物线”解读抛射运动而补李善兰之“不备”，就是其知识结构已经充实和改变的体现。

总之，李善兰的《火器真诀》对抛射运动知识的解读如同今天的“数学建模”，他用“平圆”知识重新建构了抛物线的物理意义，其目的在于更好地传播西学。其后十几位数学家用更接近兵勇们知识构成的数学语言对《火器真诀》进行解读，则是为了更快更广地传播，洋务运动这一特定的社会历史背景使得这一传播更为紧凑和深入。中算家们解读工作的意义就在于传播和普及西学。