《火器真诀》在很多书院、学校的教学中也是“必修课”，一些课艺和考课中就有反映，这部分知识通过书院教学得以传播。

《同文馆算学课艺》四卷^[77]，收录52 位学生的课艺，总计198 题。每卷之首题署“同文算学教习李壬叔先生阅定，副教习席淦、贵荣编次，肄业生熊方柏、陈寿田、胡玉麟、李逢春同校”。同文馆总教习丁韪良（W.A.P.Martin，1827—1916年）光绪六年（1880年）三月序。序称：“开馆以来十有余载，兹由副教习席淦、贵荣等将所积试卷选辑四帙，颜曰《算学课艺》。凡天文、地理、火器、测量均为切实之要端。阅者于诸生造诣亦可略见一斑。是皆李壬叔先生教授之力也”。该书当是李善兰执教期间同文馆数学教学的总结，亦为考察洋务学堂数学教育的重要史料。其中卷一就有3 题涉及《火器真诀》，题目如下：

有炮子向上直放二十秒始落，求其升高若干，并作图明其理。

有一炮其最远界二十里，移于高山顶，高出平地四十里，下测一敌营，需用四十五度方向能及之，求营距炮若干远。

有炮平速一秒五里，求最远界若干？

1892年，上海格致书院特课季课题中收录有登州道候补道员李正荣所出的考题^[78]：

问枪炮取准必用抛物线法，今以二十四生特之炮，平击敌船，当若干里？若斜向下击，或斜向上击，各当若干里？究竟下击、上击有何区别？果用何法乃能避其上击，仍不碍我下击？能精思其故得其数，而详述之欤？又以开花弹子下坠平口与平击竖口，当用何术使之不失累黍？能考其用法欤？

1895年，陕西味经书院设时务斋，分门课士，“凡有志时务之学者，无论自占何门，均需学算”。1897年，将各门学生优秀课艺结集刊刻，其中就有张秉枢的《火炮量算通法》。张氏序称：

陆君映庚《炮说》“仰、平、俯”三题，以四率比例御之，定法也。但陈君其晋跋云：“李壬叔《火器》一卷，主平圆立算，有图说而无成法”，则非也。壬叔之法，以量代算，其图说即其法。其有法无数，不以数拘也。故自序云：“依款量算，命中不难也”。试以陆君三题依法入之，得轴线高度，亦与相同。而营弁即不知算，未有不能量者，则壬叔法为适用矣。^[79]

从序的内容来看，张氏是因为不满陈其晋对《火器真诀》的评价，他认为《火器真诀》“以量代算，其图说即其法”，借用陆映庚的三题和解法，对照李善兰的原法，张氏给出自己的算法，因此称“量算通法”。味经书院院长刘光蕡评价说：

炮火以命中为贵，李氏抉其源，陆君畅其流，秉枢乃能沿流溯源，疏通证明，量算并用，而其算且省倍，于戎事尤便，为二家之调人，亦有志士也。量算施之战阵，犹有猝不及详之时，施之城垒，则量算其界，预为一册，贼知某界，发及某界之炮，贼无定而命中之处已定，真以活炮击呆贼矣。今东西时事并亟，全陕行坚壁清野法，因命刻其说于《味经课艺》中，以备有心固圉者之观览云。

1898年，由熊方柏鉴定，潘应祺、曹汝英勘覆的《佛山书院算课草》^[80]刊刻出版，其中卷十第一题“有田鸡炮，已知最远界能击八里之远，今测得远界七里或六里，当用何度？”就这一个题，选用了12 位学生的12 个算草。

1900年，时任湖北学政的王同愈将1898—1900年湖北各地经古场考生的算学考题答卷编校结集出版，名为《校士算存》六卷。^[81]其中卷三有2 题涉及抛射运动：

设炮昂六十度弹击远二千五百尺，求弹行空中离地最高点。

有炮轴昂度，有最远界求弹击之远法。以半径为一率，倍昂度正弦为二率，最远界为三率，求得四率为弹远。试作图解。

这些题的绝大部分解法来自《火器真诀》，题量虽然不大，但也可以看出抛射运动知识通过学校教学的一些传播情形。(www.daowen.com)

《算士校存》卷三目录以及其中一题的部分解答[光绪庚子湖北督学使署刊本（红印）]

叶耀元主编的《新学报》第一册、第二册（1897年8月）收录他自选的关于弹道的问题：

有炮弹最远界十里，求弹于空中每秒应行之速。

有炮弹落地远界七里又四分之一，炮轴昂度三十六度二十分，求炮弹于空中飞行时距地最高几何？

值得注意的是，《龙城书院课艺·算学》中收录的两个关于抛射运动的课草：

有炮试得平地最远界二千七百丈，置山顶于平地六十丈。问炮子能到平地若干远？（丁酉第二题沈保枢课草）

炮之平地最远界一千丈，今所欲攻者，仅距九百丈。问炮轴当低昂若干度？（乙亥第三题沈保厘课草）

在此仅就沈保枢的课草作一分析。如图5-3-2，炮在平地A 点的最远射程AB=2700 丈，现将炮的位置置于60 丈高的山顶C 处发射，弹道轨迹为抛物线CED，顶点为E，求此时平地射程AH 的距离。沈氏算草的主要步骤如下。

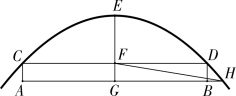
图5-3-2

因为CD 是水平最大射程，所以它的中点F 是轨迹抛物线的焦点，则CD 为通径，EF 为半通径长。法一，“准抛物线第一款：各截径之比例同于各正弦方之比”，有=，由此可以得GH，进而得到AH=GH+AG=2758.7228 丈。

法二，“准抛物线第四款例，带径（焦半径FH）方与两截径较（EG-EF）方相减开方得大正弦（GH）”，即由抛物线上某点到焦点的距离等于它到准线的距离，可知焦半径FH=EG+EF。所以GH=，从而AH可得。

沈氏在这个算草中，“准抛物线若干款”对应的定理均来自艾约瑟、李善兰合译的《圆锥曲线说》，而且可以看出他对抛物线的性质相当熟悉。更为重要的是，此时他不再依靠李善兰的《火器真诀》解题，而是直接求助于圆锥曲线的性质，对知识的运用相当自如，可见当时龙城书院的学生对圆锥曲线知识已经很熟悉，知识构成已经发生了变化。