邓钧，江西南昌人。《炮准算法图解》包含《火器演草》2 卷（1902年自序）和《火器补编》2 卷（1902年自序）。

邓氏认为李善兰“《火器真诀》以平圆通抛物线，术诚简便，但所列各款仅具图说而无题草，其用之临阵放炮之时未免多费思索”。而且前人的解读著作又“难称善本”，于是将李氏原书分为平面射击和斜面射击两种情形，还是沿用李善兰图示的办法，逐款解释，写成《火器演草》2 卷。在此基础上，邓氏认为还有一些“非平圆可通”“不藉平圆而藉抛物线”的情形，加以研究后写成《火器补编》2 卷，取意补《火器真诀》之缺。^[68]此编主要是针对《火器真诀》没有图解射程、速率和时间的情形。就其中一例进行说明。

例：已知发射角α，斜面倾角θ 及炮平面射程s，求斜面射程s′。（《火器补编》卷1 第6 款）

借用上一节图5-2-1，设V 点为抛物线顶点，过V 点作平面AX 的垂线交AX 于C 点，交斜面AI 于E 点，交切线AT 于F 点。由邓氏“准抛物线理”得

AC=CB，FV=VC，且FV∶FE=AE∶AI

“准八线理”可得(www.daowen.com)

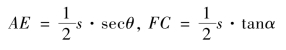
又FE=FC-EC，最后可得

这里“抛物线理”主要是应用了抛物线切线和次切线的性质，邓氏没有明确指出来自哪本著作，但这个知识点可以在《代微积拾级》卷5“抛物线”、《圆锥曲线说》卷3“抛物线诸款”以及后来的有关圆锥曲线的著作^[69]中找到。可以看出，当时这些知识已为邓氏所掌握，不再是什么难点，他已经认识到抛射运动知识有些“非平圆可通”。

1910年，邓氏的《炮准算法图解》呈献军咨处，被誉为“简而不陋，深而不晦，洵足以传世，《补编》尤能补李氏华氏之所不备”，被列为“高等算学教科书之一种”。