华蘅芳（1831—1902年）的《抛物线说》^[58] （约1860年成书）是针对《火器真诀》而写的，目的也是解读《重学》中抛射运动知识。华氏自识称：

忆余二十余岁时，阅《代微积拾级》，粗知抛物线之梗概，而《重学》中《圆锥曲线》尚未译出也。李君秋纫以所著《火器真诀》见示，余觉未能满意。因以积思所得者，笔之于书，徐君雪村为余作图，遂成此帙。

为什么华蘅芳对《火器真诀》不满意呢？他对其中的什么不满意呢？先对《抛物线说》予以简介。

《抛物线说》分两部分。第一部分论述“抛物线之理”。这部分首先根据《重学》的相关内容介绍惯性定律、重力等力学知识，并指出作抛射运动的物体当其初速度与重力方向相同或相反时轨迹是直线，否则是抛物线。其次对照图示介绍了抛物线的直径、通径、带径、准线、切线等概念以及切线与准线的一些几何性质。这些知识显然来自《代微积拾级》（1859年）卷五“抛物线”。最后还给出一个轨迹问题：借用图5-2-1，设初速度v 一定，发射角θ 在90°到0°之间变化时，子弹的轨迹为等通径的抛物线族。这些抛物线共准线，焦点在以A 为圆心、A 到准线距离为半径的圆上；顶点在一个椭圆上，其短轴为焦点轨迹圆半径，长轴为直径，且平行于公准线。华氏没有给出证明和来源，可能与上述引起李氏“忽悟”的例题也有关。

第二部分论述“抛物线之用”。这部分先给出常数“坠数（g′）”的测定方法（g′=），以及已知发射角α 和平面射程s 求初速速率v 的算法。

该算法对应的原文为：

测一秒中物之平速（v）。以物向空中若干度（α）抛出及物落至地面量得其距抛处若干远（s）。乃以半径为一率，抛角正切（tanα）为二率，抛落距（s）为三率，求得四率，以一秒中坠数（g′）除之，开方得秒数（t）。又以半径为一率，抛角正割（secα）为二率，抛落距（s）为三率，求得四率，以秒数除之，即得物受抛力一秒中行平速之数（v）。

此即

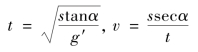
由此可得式（5.3.1）。在实际操作中，初速速率v 也是一个不易测量的数值，华氏给出一个推求的办法。此式《火器真诀》中没有论及。

之后该节指出抛物线之用“不外乎两大类：一曰设角求距，一曰设距求角”。角指的是“发射角”，距指的是“射程”。略举两例来说明^[59]。(www.daowen.com)

例1：高抛求高斜距。一率抛角正割（secα），二率抛斜两正切较（tanα-tanθ），三率平速（v），求得四率以坠率除之，寄左。一率抛角正割（secα），二率斜度正割（secθ），三率平速率（v），求得四率以寄左数乘之。即得斜上之抛落距（s′）。

此术为斜面射程s′算法，即

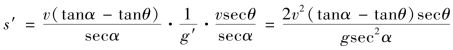
变形可得（5.2.2）式。

例2：平距求抛角。一率倍抛点距心数 [即平地最大之抛落距（smax）]，二率平距数（s），三率半径，求得四率（cosφ），检余弦表得度（φ），以加减九十度而半之，转减九十度得大小两抛角（α1，α2）。

即

此术为平面最大射程内目标的两个发射角的算法。从术文“抛点距心数”及注文“平地最大抛落距”可以看出，此术是《火器真诀》第9 款图解的具体算法，借用图5-2-3，φ 即图中的∠AOA1（或∠AOA2）。

从识语和内容可以看出，《抛物线说》重点也是解读《重学》中抛射运动知识[式（5.2.1）至式（5.2.4）与式（5.2.7）等5 式]。华氏在文中并未直接指明对《火器真诀》不满意的地方，相较于《火器真诀》，该文交代了一些力学知识，对抛物线进行了简介，将《火器真诀》图解的各量给出具体“术”——四率比例形式的算法。“术”以及“四率比例”是当时更为熟悉的数学形式。看来，华氏不满意的地方应是《火器真诀》“以量代算”的行文方式不利于学习传播。对于此，华氏另一著作《平三角测量法》^[60]的识语可作为佐证。他说：

《平三角测量法》，余于光绪丁亥年（1887年）在天津武备学堂时所辑也。学堂为演习西洋陆师而设，其中肄业之徒皆自淮军各营选来，武夫略知文字，于古今算学之书未能卒读，难与言几何代数之精，而测量之事又为行军所必需。斯时，教习算法者为卢君木斋、姚君石泉、孙君筱垞^[61]，恒苦无善本之书，朝夕授徒，使之但知其法而不必明其理。余故从西法撮取各术，冠以浅近易明之语，又列代数算式，以便仓卒翻阅，至于立术之理未暇及也，学者苟能习此亦足以致用矣。

“测量之事又为行军所必需”，弹道之学则更是必需。显然，抛射运动知识最直接的受众对象是军营的兵弁，他们连平面测量学也只能“但知其法而不必明其理”，更何况刚刚译介的抛射运动知识呢。可见，华氏将《火器真诀》的图解法改用四率比例算法重新解释，目的是再次降低抛射运动知识的门槛以便“略知文字”的兵弁们更好地接受。