李善兰的《火器真诀》^[41]是国人对《重学》抛射运动最早，也是最为重要的解读论著。他在咸丰戊午腊尽日（1859年2月2日）的自识中交代了该书的写作与《重学》有关，他说：

凡枪炮铅子皆行抛物线，推算甚繁，见余所译《重学》中。欲求简便之术，久未能得。冬夜少睡，复于枕上反复思维，忽悟可以平圆通之，因演为若干款，依款量算，命中不难矣。

《火器真诀》文字简练，共12 款，即12 个命题，每款数十、上百字，借用“圆”图解《重学》中抛射运动发射角与射程之间的5 个关系式[式（5.2.1）至式（5.2.4），式（5.2.6）]，主要内容是第7—11 等5 款。兹简介如下。

第7 款：凡推铅子所落之地必以平地最远界为根。

该款的意义在于图示平面最大射程smax。smax是一个重要参数，但不便实测，该款给出一个间接测量法：先测出大于45° 的发射角所对应的较小射程s，然后依图示可以测出smax。如图5-2-2，作RtΔTAB 使得斜边上的高AX=s，∠XAT 等于发射角α，则以TB 为直径的圆的半径即为最大射程，即r=smax。显然，s=TAcosα=TBsinαcosα=rsin2α，对比式（5.5.1）和式（5.5.3）两式，知半径即为smax。

第8 款：以最远界为半径作平圆，过圆心作地平线，止炮圆周，则九十度通弦为炮轴方向，圆心为铅子所落之处。

此款图示smax对应的发射角α0。如图5-2-2，以OA=smax 为半径作圆，OR垂直于直径，则RT 为速度切线，∠ORT 即为最大射程对应的发射角α0=45°。

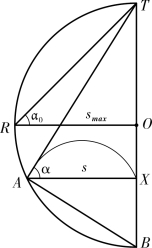
图5-2-2　由s 求smax

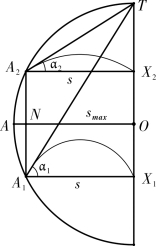
图5-2-3　s 对应的发射角

第9 款：凡地在最远界之内，则以正弦为地距炮之线，正弦分半周为二弧，二弧之通弦即炮轴之二方向。

此款图示平面射程s（＜smax）对应的两个发射角α1，α2，即图解式（5.2.7）。如图5-2-3，以OA=smax 为半径作圆，取ON=s，过N 点作OA的垂线交圆于A1，A2 两点。作X1A1 ∥OA，X2A2 ∥OA，并联结A1X1，A2X2，则∠X1A1T，∠X2A2T 即为s 对应的两发射角α1，α2。显然，α1+α2=90°，第8 款为此款的特例。

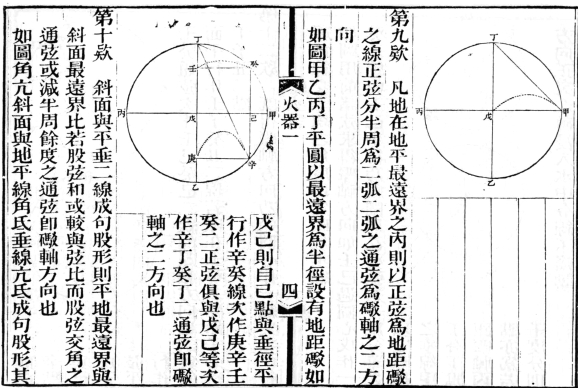
李善兰《火器真诀》第九款、第十款（续修四库全书本）

第10 款：斜面与平垂二线成勾股形，则平地最远界与斜面最远界比若股弦和（或较）与弦比，而股弦交角之通弦（或减半周余度之通弦）即炮轴方向也。

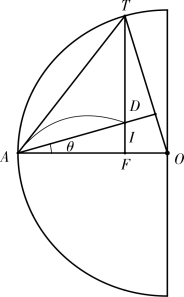
图5-2-4　smax，s′max 关系

此款图示平面和斜面最大射程smax，s′max 两者之间的关系，以及s′max 所对应的发射角。如图5-2-4，斜面倾角∠OAI=θ，过圆心O 作斜面AI 的垂线OD 交圆于T 点，联结AT。过T点作OA 的垂线交斜面于I 点，交OA 于F 点。则=1+sinθ，∠OAT 为s′max 对应的发射角。此款图示中圆半径不是smax，且s′max 不能直接图示出来，略显不足。后来卢靖在其《火器真诀释例》中对此进行了改进。

第11 款：凡地在斜面最远界内，则自最远界端量取其数作点，于此点与前款正弦平行作通弦，自通弦二端至正弦端作二线即炮轴二方向。

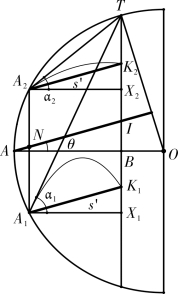
图5-2-5　s′对应的发射角

此款已知平面最大射程，图示出斜面射程s′（＜s′max）对应的两个发射角α1′，α2′。如 图5-2-5，依照第10 款 （图5-2-4）作AI=s′max，取IN=s′，过N 点作OA 的垂线交圆于A1，A2 两点，过I 作IT 垂直于OA 交圆于T点。作A1X1，A2X2 与OA 平行交IT 于点A1 和A2，则∠X1A1T，∠X2A2T 即为s′ 对应的两发射角α1，α2。若θ=0°，即得第9 款结论。简单证明如下：

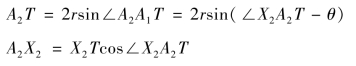
则

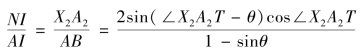
由式（5.2.2）和式（5.2.4）有

对比可知∠X2A2T 就是所求发射角，同理可证∠X1A1T 是另一发射角，且

∠X2A2T+∠X1A1T=2∠TAO=180°-∠AOT=90°+θ

满足式（5.2.7）。

李氏图解法科学性的详细证明可以参考刘钝先生的研究。《火器真诀》全书条理清楚、逻辑性强，诸款环环相扣、一气呵成，全文只有图示，没有证明，“以量代算”，抛开《重学》的力学背景知识以及代数形式的推证，用中算家自己所熟知的“圆”对抛射运动知识进行“建构”，实际上是为式（5.2.1）至式（5.2.4）以及式（5.2.6）等5 式建立了一个几何模型。现在看来，如同当今的“数学建模”。

我们注意到，抛物线的知识当时还只是在《代微积拾级》中以解析几何的方式进行比较全面的论述^[42]，当时另一部介绍圆锥曲线知识的著作《圆锥曲线说》还未译出。它们于国人而言还是一个比较陌生的领域。

我们注意到，由式（5.2.5）证明轨迹曲线为抛物线的数学基础在卷11中没有说明，整个《重学》也没有。大约7年之后的金陵版《重学》（1866年）所附的《圆锥曲线说》卷三“抛物线”第8 款的推论倒是可以作为依据。该款称：(www.daowen.com)

（抛物线）切线内任取诸点作诸线正交通弦，诸线在曲线外一分之比若切线诸截分方之比若通弦截分方之比。

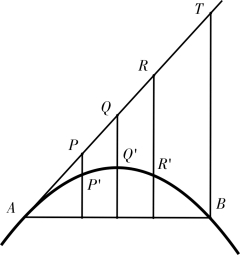
图5-2-6　《圆锥曲线说》卷三“抛物线”第8 款

如图5-2-6，AB 为抛物线的弦，AT为过A 的切线，过切线上任意两点P，Q作AB 的垂线交抛物线依次为点P′，Q′，这个命题的结论为：AP2∶AQ2=PP′∶QQ′。

该款逆命题成立，即若AB 为曲线的弦，P，Q 为过A 点的切线AT 上任意两点，若AP2∶AQ2=PP′∶QQ′，则P′，Q′所成的曲线轨迹为抛物线。

此款的证明要用到卷三“抛物线”前面的定理命题。根据这个命题，可以由式（5.2.5）证明图5-2-1中轨迹曲线APB为抛物线。因此，学界一般认为《圆锥曲线说》是为解释《重学》的数学内容而译。

同样，由式（5.2.6）也可以证明抛物轨迹曲线为抛物线，但其数学基础当时能在《代微积拾级》（1859年）中找到。研究表明，《代微积拾级》在1856年底就译成^[43]，但当时只有包括译者的少数人知道，该书是“咸丰己未孟夏之月”才公开刊行，按“孟夏之月”指四月，咸丰己未四月初一为1859年5月3日，在李善兰写作《火器真诀》的时间（咸丰戊午腊尽日，1859年2月2日）之后。

因此，就抛射运动这几款而言，其数学基础在《重学》初版之时国人一般无从知晓。但是，如第一节所述，让炮兵们尽快掌握抛射运动知识又迫在眉睫，因此李善兰认为必须“求简便之术”同时还得达到“命中不难”的实际效果。所以李氏“以平圆之理”去解读抛射运动知识，以便让更多的人理解抛射运动的规律。而圆的知识对于当时的有一定数学基础的人而言不是什么难点，一定程度上说，“以平圆通之”也是权宜之计。

至于李氏为什么“忽悟可以平圆通之”，我们认为《重学》卷11 后附例题的第4 题应该对李氏有所启发。该题为：

假如于甲点将多物用同速抛出，行于一个面上之各方向线，历若干秒，物行各至何处？

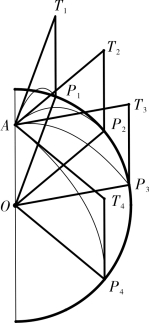
图5-2-7　《重学》卷11 例题4

如图5-2-7，从A 点沿平面任意方向以相同的速率v 抛出若干物体Pi，问t 时间后它们的位置。书中给出的解答为“诸物俱在平圆周”。如图最后各Pi 在以O 为圆心，vt 为半径的圆周上，其中O 点在A点的下方，且OA=即物体在t 时间内自由落体运动时的距离。该题最后还指出“设抛物方向不在一个面上，则历若干秒，各物俱在立圆周”，“立圆周”即球面。这句话指出：若方向是空间任意的，则各点Pi 在以O 为球心，vt 为半径的球面上。

如图5-2-7，反过来看，若以适当的发射角和初速度，从Pi 点发射炮弹，则均能命中目标A。这与《火器真诀》第11 款（图5-2-5）有相通之处，可能是此题中“平圆”这个李氏所熟知的知识点引起他的“忽悟”。

在此，顺便介绍下后面两个例题。第5 个例题在第4 题基础上用几何的方法证明子弹以相同初速度不同发射角的弹行轨迹（抛物线）的顶点的轨迹是椭圆。第6 个例题接着证明这个弹行轨迹的最大射程端点的轨迹是抛物线，这实际上是证明了以相同初速度不同发射角的弹行抛物线族的包络是以炮位为焦点的抛物线。这个证明最早由数学家约翰·伯努利在1692年给出。^[44]这也说明惠威尔的《初等力学教程》的确还带有明显的数学 （或说几何）特点。

总之，通过李善兰的解读和重构，与枪炮有关的抛射运动知识门槛得以降低，《火器真诀》也因此成为之后中算家理解抛射运动知识的主要文献。^[45]李善兰也因此获得很高的社会声誉，俨然成为通兵法的儒生。李氏的外甥崔敬昌在《李壬叔徵君传》中说：

嗣金陵大营震撼，庄愍（徐有壬谥号庄愍公）喟然曰：测量推步，精其术可以通兵法，壬叔在此，岂遂作退守计乎？一日，具币遣使，敦促就道，辞不获已，力疾行。^[46]

咸丰十年（1860年）6月，徐有壬镇守的苏州在太平军的攻击下危在旦夕，李善兰还与龚孝拱（龚自珍之子）、王韬商议企图向英法公使“借师”解救徐氏。^[47]

王韬在《火器真诀》完成的当月就阅览一过，他在咸丰九年正月二十日（1859年2月22日）的日记中记载：

壬叔近著一书，曰《火器真诀》。谓铳炮铅子之路，皆依抛物线法，见其所著（译）《重学》中，而亦能以平圆通之。苟量其炮门之广狭长短，铅丸之轻重大小，测其高下，度其方向，即可知其所击远近，发无不中。炮口宜滑溜，铅丸宜圆灵，外可加髹漆，则永不铁锈。欲知敌营相距几何，则以纪限镜仪测之，然后核算，宜纳药若干，铅丸若干，正至其处，无过不及。西人所以能获胜者，率以此法，其术亦神矣哉。^[48]

后来王韬在同治二年（1863年）完成了《火器略说》[刊于光绪七年（1881年）]，其中“用炮测量说”一节再次论道：“近海宁李善兰曾著《火器真诀》，谓弹去皆依抛物线从高下坠，有一定之准可算。”李鸿章曾说：“弹之远近疾徐，炮之高下缓急，此用炮者之事也，其中皆有至当一定之理，非可浅尝而得。”^[49]《火器真诀》印证了并一定程度上解决了李鸿章所说的“一定之理”。

薛福成曾在其日记里这样描述枪弹射击距离的原理，他说：

枪炮取准，法至不一，而炮准尤难。然不外无定法、有定法二者而已。……何谓有定法？盖即弹路所成之抛物线，可以算术得其高低远近之数。夫弹之所以必循抛物线者，系合三种力所成，为势所必然之重学理，非可强也。一为弹行本重速力，一为地心吸引力，一为空气阻力，合而较之，而抛物线之理得矣。抛物线之理得，则弹所能及之道里丈尺，不难推算而知。所谓有定法，其数可测者也。^[50]

咸丰十一年（1861年），曾国藩率军攻陷皖南重镇安庆后着手组织人手研究枪炮、轮船、制造，创设安庆军械所，并向各方招揽科技人才，充实力量。经郭嵩焘推荐，李善兰进入安庆军械所，成为曾国藩幕府成员，《火器真诀》是其一个重要的凭借。张文虎曾在《怀人十五首》其中一首中说（中括号内为原注，双行小字，下同）：

谈天近方厌，投笔起从戎。长揖见节相，上策论火攻。请以径路刀，扰酒留犂钟[李善兰时从军]。^[51]

此诗将李善兰的译著《谈天》和著作《火器真诀》嵌入。

同治二年（1863年）十月王韬致信给身处广州的吴嘉善，介绍几位故人的近况时提到李善兰说：

沪上故交，闻皆无恙。……李君壬叔，献策军中，谈兵席上，兹在皖南，未闻奇遇，岂《火器真诀》不遑一试其所言耶？^[52]

李善兰到安庆一年后，向曾国藩推荐了他的两位朋友张文虎和张斯桂。曾国藩在同治二年五月二十一日的日记中记载：

又李壬叔带来二人，一张斯桂，浙江萧山人，工于制造洋器之法；一张文虎，江苏南汇人，精于算法，兼通经学、小学，为阮文达公所器赏。^[53]

同年，李善兰还向曾国藩推荐了中国近代第一位毕业于美国耶鲁大学的留美学生容闳。加上之前到达的徐寿、华蘅芳、方俊谟等人，当时曾国藩幕府可谓人才济济。张文虎离开安庆即将赴金陵南京前住在任家坡宾馆，宾馆是为安庆军械所原址，他写诗回忆了当时的情景：

武库南城上[宾馆在任家坡，为节相内军械所]，遗封皖伯都，江山环列障，天地入红炉，述学多同志，来游各异途，周张兼比屋，乡语不离吴[同居华蘅芳（若汀）、徐寿（雪村）皆无锡人；李善兰（壬叔）海宁人；叶圻（云岩）、钟瑜（西白）皆嘉兴人；而比邻周缦云侍御（学浚）、陈小舫太守（庆瀛）皆湖州人也]。^[54]

这“指点江山，激扬文字”的情形，可以说是当时士人积极入世参与自强运动的一个时代缩影。