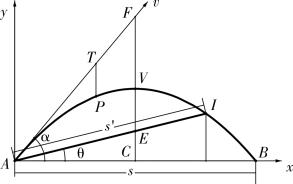
图5-2-1

《重学》^[39]专论抛射运动的卷11 开篇指出“凡物抛于空中，除垂线外，任何方向为地心力所加，必令物行于曲线”，共7 款，最后配有6 个例题。每款先是给出结论，然后证明，这是明显的演绎风格。如图5-2-1，AX 为平面，AI 为斜面，倾角为θ ^[40]。子弹从A 点发射，初速度大小为v，发射角为α，重力加速度为g。曲线AVB为子弹轨迹，P 为轨迹上任一点，其竖直高度为y，水平距离为x，对应的时间为t。设平面射程AB 为s，斜面射程AI 为s′。平面能达到的最大射程记为smax，斜面能达到的最大射程记为s′max，对应的最大射程发射角分别记为α0 与α0′。h 为子弹以速度v 竖直发射达到的高度，则h=。各款简介如下。

第1 款：“从某点将物抛出，以某速行于某线，求地平面上的抛物界。”

此款相当于给出平面射程的算法：

并在推导过程中给出了P 点位置的竖直高度和水平距离的算法：

第2 款：“从某点将物抛出，求斜面上抛物界。”

此款给出了子弹斜面射程的算法：

第3 款：“用某速抛物，当用何方向令抛物界最大。”

此款推导出了平面和斜面两种情形的最大射程算法以及对应的发射角。

第4 款：“抛线界用抛高求等数。”

此款给出式（5.2.1）至式（5.2.3）用高度参数h 表达的算法，如s=2hsin2α 等。

第5 款：“抛物线即圆锥上之单曲线。线上任取何点，欲知其抛速若干。”(www.daowen.com)

此款以综合几何的方法证明子弹轨迹曲线为抛物线。TP 垂直于平面AX，T 在速度切线AT 上，则有

由这个关系式证明轨迹曲线AVB 为“圆锥上单曲线”，通径等于4h。

这一命题对应的英文原文为：

The curve described by a projectile is a parabola，and the velocity of the projectile at any point is that acquired by falling from the directrix of the parabola。

对照英文，“单曲线”系《重学》中parabola （抛物线）的译名，此处的“抛物线”指的是抛射物体的轨迹，现今parabola 的译名“抛物线”是经过《重学》沉淀之后的译名。

第6 款：“抛物线用垂线及地平线求等数。”

此款推导出抛物轨迹曲线的解析方程，从解析几何的角度证明轨迹曲线为抛物线。这一命题的英文原文为：

To find an equation to the curve referred to horizontal and vertical co-ordinates。

如图5-2-1，以A 点为原点，AX 为横轴，AY 为纵轴建立坐标系，点P的坐标为（x，y），抛物曲线轨迹方程为：

第7 款给出平面情形时最大射程内某一射程s（＜smax）与其对应的发射角φ 的关系式：

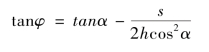
最后所配的6 个例题中的例1 指出：最大射程内（平面s，斜面s′）的某一目标对应有两个发射角α1，α2，则它们对称于各自最大射程发射角α0，即

式（5.2.1）至式（5.2.4）以及式（5.2.7），这5 个关于射程与发射角的算法是中算家关注的重点和解读的出发点。