周达（1879—1949年），字美权，安徽建德人。周达对容圆问题有独到的研究，其《平圆互容新义》（1900—1901年）是讨论容圆圆心轨迹的专著，首次连载于《亚泉杂志》第4、5、6 册上。^[29]李迪先生较早注意到周达的这部著作，作出了较为详细的论述，指出周氏是要运用圆锥曲线解决复杂的平圆互切问题。^[30]本书在参考前人的研究的基础上，注意到周氏这部分工作与《亚泉杂志》的关联。周氏在序（1900年）中称：

平圆交互相容，其理极繁赜杂糅，不可以平常几何之法驭之，间尝深思而得其故。知须藉径于圆锥三曲线，理幽趣奥，实于形学中别开一径，不可无专书以发明之。爰为之首列三款以明其原，次设诸题以竟其用。凡向之所谓繁杂赜糅无法可驭者，今皆视为坦途矣。三曲之妙用，真不可测哉。

周氏的目的是解决容圆问题，他发现容圆圆心轨迹就是圆锥曲线，共列出了三款，简介如下。

第一款：如图4-3-10，设不等两圆相交，或内切，或内含，在两圆间作切圆，使诸圆内切于一圆，外切于另一圆，则诸切圆圆心的轨迹为椭圆。

图4-3-10

第二款：如图4-3-11，设两圆相交，或相切，或相离，动圆与两定圆均内切或均外切，则其圆心的轨迹为双曲线（只有一支）。

图4-3-11

第三款：如图4-3-12，设一圆与一直线相离，或相切，或相交，动圆与定圆及直线均相切，其圆心的轨迹为抛物线。

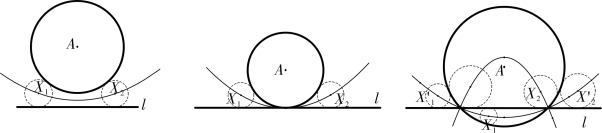
图4-3-12

周氏利用圆锥曲线的定义对每一款均给出了证明，并且给出了各轨迹曲线的参数，其结论和证明都是正确的。周氏文中还列举10 个练习题，“设诸题以竟其用”。现以第7 题为例说明如下：

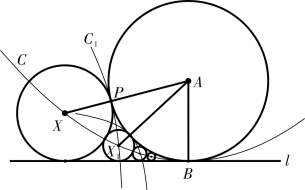
图4-3-13

如图4-3-13，⊙A 与直线l 相切于B 点，在圆与直线之间作无数容圆，它们本身相互外切。若已知第一个容圆圆心X，求其余容圆圆心。

解法为：首先以A 为焦点，AB为轴，B 为顶点作抛物线C；然后联结AX，设⊙A 与⊙X 公切点为P，以A，X 为焦点，AX 为轴，P 为顶点作双曲线一支C1，C1 与抛物线C 的交点X1 即为相邻容圆圆心。以下类推。

周氏关注容圆问题可能与《亚泉杂志》有关。《亚泉杂志》于光绪二十六年（1900年）十月创刊，共出10 册。第1—4 册为半月刊，第5 册起改为月刊。每册均设有“算学问题（答）”的栏目，这个栏目连续刊载了多个有关容圆圆心轨迹的互动问答。

第1 册提出问题（1）^[31]：

弧矢形内切多圆，联多圆心成一曲线，即抛物线也，且此抛物线之心必与弧矢形之圆心同在一点。试证之。

第2 册刊出了题（1）的证法，并且提出新的问题（2）：

以有定长之直线为弦，上作多勾股形，联诸形之容圆心，必成一曲线。试问其为何种曲线，其性情如何，其方程式如何。

第5 册刊出两位读者的解法，并且提出新的问题（3）：

于由定长之直线上作无数三角形，其顶角均相等，则联此诸形之内容圆心成一曲线。试问其为何种曲线。

第6 册刊登周达对题（3）的解法，他还指出（2）是（3）的特例，并且周达还提出了一个问题（4）：

以椭圆之两心连线为底，以椭圆周内任一点为顶点作诸三角形，联诸三角形之内容圆心必仍为椭圆。求其证。

此题是题（3）的推广。

第7 册指出题（3）仍有很多读者寄来解答，并刊出其中一简捷解法。第10 册刊出周达本人给自己提出的问题（4）的证法。

周达的《平圆互容新义》就是发表在第4—6 册上，明显是要给予容圆问题一个统一性的理论性的解答，他撰写这部著作的动机可能来源于第1 册的提问。

周氏对容圆问题有很深的研究，后续著作有《巴氏累圆奇题解》（1904年）和《圆理奇侅》（1907年）。前者解决了帕普斯问题（Pappus’ Problem）并作了推广，后者主要讨论容圆问题中切点的轨迹问题。^[32]如他证明了在图4-3-10右图中，若所容圆相互两两外切，则切点为轨迹是一个圆，圆心则是已知两圆的连心线与某个容圆与已知两圆切点连线的交点。^[33]

由以上论述，我们认为：

第一，根据容圆问题已知两圆或已知圆与直线的位置关系[相交、相切、相离（内含、外离）]，以及所容圆的位置关系（内切、外切），共有9 种情形。黄宗宪考虑了6 种情形，没有考虑线圆相离、两圆内含、两圆外离等3种情形。他研究的出发点是封闭的三角形。蒋维钟在黄氏的基础上补充了线圆相离、两圆内含等两种情形。他研究的出发点是曲线平分“夹角”。周达讨论了全部的9 种情形，方法全面且具有系统性，具有现代意义。《亚泉杂志》称周氏成果为“精心妙义”。

第二，及至晚清，容圆问题类型丰富，有突然之势，很多并非中算固有的容圆问题得到推广，原因主要有二。

其一，容圆问题是传统数学关注的问题。黄宗宪在《容圆七术》序中将他的研究直接指向李冶的《测圆海镜》，他说：

昔李乐城（指李冶）得洞渊九容之说，反复推求，唯穷偏勾股容圆之理，其所撰述后世珤之。今天下不尠好学深思之人，试即各术而推广之，……容圆必不出此范围矣。不特能竟古人未竟之绪，洵可施诸实用者也。^[34]

华世芳在龙城书院任算学教习时，常常以容圆问题来考课学生，也是在传统数学中能找到根源，他说：

《容圆九术》导源洞渊，敬斋（指李冶）继作演为《海镜》。是时，机缄初辟，默守一隅，勾股以外未闳诀，旨利、伟西来，徐、李笔译《几何》《代数》，次叙流布内容之法，日益繁多。余以丙申（1896年）戾止龙城时拈圆理课程，学子……触类引申，妙有新得。寒暑几更，裒然成稿。^[35]

其二，显然与西方数学传入有关，特别是一些经典的几何难题，如阿波罗尼问题、马尔法蒂问题、卢卡斯圆问题以及帕普斯问题。这些问题的出现得益于《格致汇编》《中西闻见录》《亚泉杂志》等杂志的译介以及同文馆天文算学馆的推介。解法中涉及的位似法、反演法等尺规作图法属于近代欧氏几何内容，这部分知识在晚清的输入与传播有待进一步研究。

应注意的是，18世纪中期以降，和算的“累圆术”已经论及类似阿波罗尼问题的容多圆的问题^[36]，有资料显示一些成果也传入晚清。日本加悦传一郎的《算法圆理括囊》（1852年）有题：

今有如图，线上载大小二圆，其交罅容不等六圆。大圆径若干，小圆径若干。问天地圆径术如何。^[37]

按所容六圆，小者称“天圆”，大者称“地圆”。该书传入的年代与经过不详，日本嘉永五年（1858年）序成，晚清同治十三年（1874年）刊入《白芙堂算学丛书》，由黄宗宪校算。黄氏的《容圆七术》亦将容圆称为“天圆”，应该对加悦氏有所借鉴。另，日本会天安明的 《算法天生法指南》（1810年）收入《古今算学丛书》（1898年），其中也有一些“累圆术”问题。此外，叶耀元的《容圆切点图解》（1898年）自序曾称：

己丑（1889年）之秋，元入都赴京兆试。一日造同乡王绂卿^[38]主政之庐，其喆嗣孝胥^[39]兄口述是图，谓见之于同文馆，莫知其所出。……前岁与英儒艾约瑟君相质证，谓尝于多录亩书（指托勒密）中见有相类之图，嗣复询诸美儒潘慎文君，以为得未曾有。然刘师省庵夫子（指刘彝程）则曰，曾于一册日本书中见多图，间有与此相类者，往往有图无说，阅书者每无从索解。甲午（1894年）之秋，有友自扶桑返，袖出古算书一册，谓向横滨旧书坊购得者，内载图甚夥，自加减、诸分以迄少广、勾股、盈朒、差分，为图不下七百余，而粗鄙浅陋，多无精义，更无与此类者。^[40]

有研究表明，《算法圆理括囊》在中国几乎没有什么影响。^[41] 《算法天生法指南》中累圆算题较之《算法圆理括囊》多，但所用方法是“点窜术”，考虑到《古今算学丛书》属于丛书，《算法天生法指南》在丛书“象数第三”天元部分，估计是编者觉得“点窜术”与中国天元术类似，因而将该书编入丛书，但就其布算方式和语言习惯来看，该书在中国影响有限。

第三，晚清中算家关于容圆圆心轨迹是圆锥曲线的探讨，是吸收西方数学知识的表现。如第一章所述，晚清圆锥曲线知识主要有三个来源：《代微积拾级》（1859年）中的解析几何内容，《圆锥曲线说》（1866年）以及教会学校编译的教科书《圆锥曲线》（1893年）和《代形合参》（1894年）。运用圆锥曲线定位容圆圆心的方法，可以看成是圆锥曲线知识被中算家理解、吸收到一定程度后的自然显现，是它们被中算家内化为知识构成的结果。(www.daowen.com)

【注释】

[1]刘钝：《夏鸾翔对圆锥曲线的综合研究》，《第三届国际中国科学史讨论会论文集》，北京：科学出版社1990年版，第12-18 页。

[2]刘钝：《夏鸾翔对圆锥曲线的综合研究》，《第三届国际中国科学史讨论会论文集》，北京：科学出版社1990年版，第12-18 页。

[3]杨兆鋆，浙江乌程（今湖州）人，1854年生，1871—1877年在京师同文馆学习，当时的算学教习是李善兰。杨氏的《须曼精庐算学》于1898年撰成，1916年由嘉业堂刊刻，收入《吴兴丛书》。见王全来：《清末数学教育的一个案分析——李善兰数学工作对杨兆鋆的影响》，《广西民族大学学报》（自然科学版）2008年第3 期，第27-30 页。

[4]刘钝：《梅文鼎在几何学领域中的若干贡献》，梅荣照主编：《明清数学史论文集》，南京：江苏教育出版社1990年版，第182-218 页。

[5]关于清代勾股术的发展，参阅赵彦超：《明清时期勾股算术的发展与西学的影响》，中科院自然科学史研究所博士学位论文，2005年。

[6]狄考文曾感慨道：“夫勾股之理固属紧要，然亦不过形学之一端。”见（美）罗密士著，（美）狄考文选译，邹立文、刘永锡同述：《形学备旨·狄考文序》，光绪十一年（1885年）美华书馆铅印本。

[7]冯立昇、牛亚华：《李善兰对椭圆及其应用问题的研究》，李迪主编：《数学史研究文集》第三辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1992年版，第100-111 页。

[8]冯立昇、牛亚华：《李善兰对椭圆及其应用问题的研究》，李迪主编：《数学史研究文集》第三辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1992年版，第100-111 页。

[9]Heath，T.A History of Greek Mathematics.Vol.Ⅱ.New York：Dover Pulication，Inc，1981，p.182.

[10]（英）牛顿著，王克迪译，袁江洋校：《自然哲学之数学原理》，北京大学出版社2006年版，第49 页。

[11]钱宝琮：《中国数学史》，北京：科学出版社1981年版，第175 页。

[12]李兆华：《中国数学史基础》，天津教育出版社2010年版，第61 页。

[13]李文铭：《清末黄宗宪的〈容圆七术〉初探》，《自然科学史研究》2004年第3期，第251-256 页。

[14]李兆华：《晚清算学课艺考察》，《自然科学史研究》2006年第4 期，第322-342 页。

[15]陈叶祥、萧文强：《“马尔法蒂问题”在19世纪的中国——一则中国人学习西学的小故事》，《自然科学史研究》2014年第1 期，第64-69 页。

[16]李迪：《中国现代数学的先驱者周达》，李迪：《中国科学技术史论文集》第一集，呼和浩特：内蒙古教育出版社1991年版。

[17]高红成：《晚清数学家对容圆问题圆心轨迹的理论探讨》，《内蒙古师范大学学报》（自然科学汉文版）2015年第6 期。

[18]许康、寥杰初：《近代最早赴欧的数学家黄宗宪身世述略》，《中国科技史料》1990年第2 期，第35-44 页。

[19]（清）黄宗宪：《容圆七术》，下卷，《古琴古砚斋算学》，梅城知足堂本，光绪二十二年（1896年）。

[20]（清）蒋维钟：《曲线新说》，版权不详，华蘅芳1899年序，中科院自然科学史研究所图书馆有藏。

[21]赵统：《试述江阴南菁书院的治学特点》，《南京晓庄学院学报》2005年第2 期，第113 页。

[22]（清）黄耀奎：《抛物释容》，《东观裔算学·二》，经心精舍本，光绪丙申（1896年）。

[23]（清）叶耀元：《形学补编》，《古今算学丛书·第三》，算学书局本，光绪二十四年（1898年）。

[24]（清）华世芳：《龙城书院课艺（算学）》，刊本，光绪二十八年（1902年）。

[25]卢卡斯圆问题，即求作三个圆两两外切的圆，与已知三角形的外接圆分别内切于三个顶点。Reyes，W.The Lucas circles and the Descartes formula，Forum Geometricorum，2003，vol.3，pp.95-100；Moses，Peter J.C.Circles and Triangle Centers Associated with the Lucas Circles，Forum Geometricorum，2005，Vol.5，pp.97-106.

[26]陈叶祥、萧文强：《“马尔法蒂问题”在19世纪的中国——一则中国人学习西学的小故事》，《自然科学史研究》2014年第1 期，第64-69 页。

[27]支宝枬主编：《上虞算学堂课艺》，卷下，经正书院刊本，光绪二十七年（1901年）。

[28]李兆华：《晚清算学课艺考察》，《自然科学史研究》2006年第4 期，第322-342页。

[29]（清）周达：《平圆互容新义》，杜亚泉主编：《亚泉杂志》，第4 册[光绪二十六年（1900年）十一月]、第5 册（光绪二十六年十二月）、第6 册[光绪二十七年（1901年）正月]。

[30]李迪：《中国现代数学的先驱者周达》，李迪：《中国科学技术史论文集》第一集，呼和浩特：内蒙古教育出版社1991年版。

[31]题号为本书所加。

[32]劳汉生、廖世发：《周达〈圆理奇侅〉简析》，《科学技术与辩证法》1991年第1期，第43-46 页。

[33]周达：《圆理奇侅》，中国科学社印行，1938年，第32-34 页。

[34]（清）黄宗宪：《容圆七术·自识》，《古琴古砚斋算学》，梅城知足堂本，光绪二十二年（1896年）。

[35]华世芳：《容圆通义》序，沈保枢：《容圆通义》，阳湖沈氏算学初刻本，辛丑（1901年）。

[36]李俨：《日本数学家（和算家）的平圆研究》，《自然科学史研究》1982年第3期，第208-214 页。

[37]（日）加悦传一郎：《算法原理括囊》，同治十一年（1872年）《白芙堂算学丛书》本，页十三。

[38]王绂卿（1848—1895年），名颂蔚，江苏长洲（今苏州）人。早年师从冯桂芬，光绪六年（1880年）庚辰进士，改庶吉士进翰林院，散馆改户部主事，补军机章京。有四子五女：长子王季烈、次子王季同、三子王季点、幼子王季绪；长女王季昭、次女王季茝、三女王季玉、四女王季山（中国现代著名物理学家何泽慧之母）、幼女王季常。王氏为苏州名门望族。

[39]孝胥疑为王季同。王季同（1875—1948年），名季锴，字孟晋，号小徐。小徐与“孝胥”谐音。王季同1895年在京师同文馆天文算学馆毕业后留馆任教，是继李善兰、席淦之后的第三位算学教习。数学著作有《九容公式》一卷、《泛倍数衍》一卷、《积较补解》一卷等。论文《四元函数的微分法》1911年7月发表在《爱尔兰皇家学会汇刊》，是迄今所知的第一篇国人正式发表的现代数学论文。（郭金海：《王季同与〈四元函数的微分法〉》，《中国科技史料》2002年第1 期，第63-69 页。）

[40]（清）叶耀元：《形学补编·自序》，《古今算学丛书·第三》，算学书局本，光绪二十四年（1898年）。

[41]徐泽林、张娜：《中国刊刻的第一本和算书著作〈算法圆理括囊〉》，《中国科技史杂志》2007年第1 期，第24-46 页。