蒋维钟（1868—1899年），江苏常州人，字岳壮，所著《曲线新说》承黄氏之说。该书出版年代不详。华世芳序称：“蒋生岳壮，静默而好深湛之思，丙申（1896年）问算于余，愈年所学大进，同学中罕有及者。”^[20]可知蒋氏曾是华世芳在龙城书院的学生，《龙城书院课艺（算学）》收有蒋氏6 个课草。他还曾在江阴南菁书院学习过^[21]。蒋氏1899年殁于肺病，英年早逝，《曲线新说》是其遗稿一种（另还有《堤积术辩》1 卷），由其弟蒋维乔（1873—1958年，曾任东南大学校长，中国近代著名教育家）筹资出版。华世芳对该书内容解释道：

《曲线新说》者，所以驭容圆之变也。自新化黄玉屏著《容圆七术》而世始知抛物线能分平圆与直线、相交相切之角。生闻其说，因此而悟双曲线……，继又悟得椭圆线……，且双曲线……。

可见，《曲线新说》是蒋氏学习《容圆七术》的心得之作。

《曲线新说》有两小节：“双曲线取圆心”和“圆锥三曲线之用”。“双曲线取圆心”（此处“双曲线”指的是两种曲线）论道：

抛物线能分平圆与直线之交角，所以平圆与直线之交角内容圆，作抛物线必过其心；双曲线能分两不等圆外相切之交角，所以两不等圆相切之交角内容圆，作双曲线必过其心。

“圆锥三曲线之用”中论述道：

抛物线能平分平圆与直线相交相切之角，因此悟得双曲线能分两不等圆外相切之角；今又悟得椭圆能分两不等圆内相切之角，且双曲线又能分两不等圆相交之内角，而椭圆能分两不等圆相交之月形角。

蒋氏悟得的这些结论与黄宗宪“容圆用规绘捷法”命题2 和命题6 实质相同，但他均运用圆锥曲线的性质给出各结论的证明。他将关注点从弧线三角形容圆转向曲线之用——“平分”弧线（弧弧）角，而且他还对黄氏捷法有所发展，这从他给出最后一例题可以看出，该题如下。(www.daowen.com)

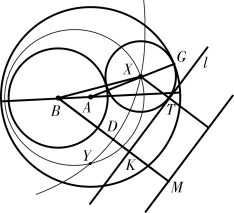
图4-3-6

如图4-3-6，两圆⊙A （a）、⊙B（b），（a＞b）内含，直线l 与大圆⊙A 相交，与小圆⊙B 相离，求作一圆与两圆和直线均相切。蒋氏给出的作法是：

首先以A、B 为焦点，以两圆半径和a+b 为长轴作椭圆。其次，过B 作BM⊥l 交l 于K，取KM=b。以BM 中点D 为顶点，以圆心B 为焦点作抛物线。椭圆与抛物线的交点X，Y 即为所求圆的圆心。一般情况下，所求圆为两个。蒋氏还给出了证明。

应注意的是，此题中直线l 与小圆⊙B 的位置关系是相离，⊙A、⊙B 相离（内含），这两种情形（线弧相离和弧弧相离）在黄宗宪“容圆用规绘捷法”中并没有论及。蒋氏在此题最后注称“圆锥三曲线不但能分相交切之角，即相离处亦能平分之”。这是蒋氏的新发现。华世芳称赞“此皆昔人未发之蕴，西书未言之理。生以精思得之，其颖悟为何如哉”。

另外，汉阳黄耀奎因解答两湖书院课士题中“弧矢容圆、象限容圆、切割线容圆”等题，悟得“抛物线之理可一以贯之”，写下 《抛物释容》（1896年）^[22]，共6 题10 图，所用方法与黄宗宪命题1 和命题6 相当。叶耀元著有《容圆切点图序》（1897年），该书收入《古今算学丛书》作《形学补编》^[23]，他证明了线圆相交时容圆的切点轨迹是圆，而圆心轨迹则是抛物线。