杨兆鋆是李善兰任京师同文馆算学教习时的学生，数学才能深得其师的赏识。杨氏在其《须曼精庐算学》卷一“椭曲同诠”（共20 题）中讨论了4个求椭圆焦点的作图问题，李善兰的《椭圆拾遗》卷二均有讨论，但在具体的作法上杨氏有些创新。

如第9 题：

椭圆有最卑点（A）及一心（F1），有周上任一点（P），求余一心（F2），其法若何。

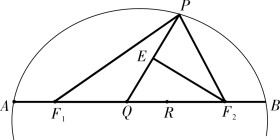
图4-2-14

该题与李善兰的《椭圆拾遗》卷二第21 款（Ⅰ）同，杨氏的作法要更为简洁。

杨氏的作法如下，如图4-2-14：

（1）在AF1 的延长线上取点Q，使得AQ=F1P-F1A（即卑径较）。

（2）联结PQ，作PQ 的垂直平分线EF2 交AF1 的延长线于点F2，点F2 即为所求。

他又研究了6 个求双曲线焦点位置的问题，这些问题均为已知双曲线的一个焦点和其他一些条件，用作图方法求另一个焦点。题目如下：(www.daowen.com)

双线有一心，有最近点，有曲线上一点，求余一心，其法若何。

双线有一心，有曲线上二点，其一点并知切线，求余一心，其法若何。

双线有本面心，有三切线，俱不知切点，求对面心，其法若何。

双线有对面心，有本面三切线，不知切点，求本面心，其法若何。

双线有最高点，有本心，有本周上一点，求外心，其法若何。

双线有最卑点，有本心，有本周上一点，求外心，其法若何。

这6 个作图题主要应用《圆锥曲线说》中“双曲线”第五款“自二心作二线交于曲线界，二线之较与长径等”和第九款“二心至切点作二线，与切线之交角必相等”作图。这些问题在李善兰作图时均有所论及讨论，杨氏只是给出了具体的作法，在此不作详细论述。杨氏对圆锥曲线焦点作图的研究，在一定程度上也反映出京师同文馆的数学教学成果。

在圆锥曲线知识传入中国的第二个阶段，《几何原本》（前六卷）已翻译出版了两个半世纪，后九卷（1857年）也得以翻译出版。《代微积拾级》和《圆锥曲线说》传入了比较完整系统的圆锥曲线知识。至此，中算家面临的几何远非清中叶所认识的“勾股即几何”那么简单了。由于天文学上的需要，从《历象考成后编》开始，中算家们对椭圆轨道问题很是热衷，认识也逐渐深刻。如果说徐有壬的《椭圆正术》仅仅是对《历象考成后编》方法上的改进的话，那么李善兰所得式（4.2.1）、式（4.2.2）则可视为对椭圆轨道问题本质的把握，也正是在这两式的基础上，李氏后来得到了椭圆极坐标方程的级数表达式（详细讨论见本书第三章第四节）。而他对圆锥曲线焦点作图（有些虽属不完全尺规作图）的成果则可视为对综合几何方法的掌握，这些表明中算家对几何的认识逐渐深刻。至于夏氏对圆锥曲线综合研究的成果，竟得到了触及近世综合几何的成果，则明显已经在传入的几何之上有所超越了。