中国传统数学中并无尺规作图理论，尺规作图是随汉译《几何原本》（前六卷，1607年）而传入中国的。尺规作图就是用直尺和圆规作几何图形，是由欧氏几何学确立起来的几何学基本方法。欧几里得的《几何原本》规定了直尺和圆规的五条效能：（1）直尺能作直线；（2）圆规能作圆；（3）若两直线相交，则能作出交点；（4）若一个圆经过另一个圆的内部和外部的点，则两圆一定有两个交点；（5）若一直线经过一个圆的内部点，则直线与圆有两个交点。在尺规的这五条效能下，可以实现平面几何中绝大部分的作图问题，进而解决几何量的计算问题。《几何原本》前六卷所有问题均是采用尺规作图方法解决的。《数理精蕴》（1723年）上编卷四即《几何原本》第11—12 章对几何作图法进行具体的讨论，涉及如比例线段、中垂线、相似形、等分圆等内容。《代微积拾级》（1859年）卷二“作方程图法”谓“作几何之图以显代数式之数”，讨论了一些基本的作图题。《形学备旨》（1885年）“凡例”中要求“学此书者必用心习画图之法，使其正斜不差，远近毕肖”，因为“图对而理自明，图误则理亦随之晦矣”。卷五“求作”涉及35 个题，主要依据“开端”中六种“可作”（公设）求作一些简单的图形，如线段的中垂线、角平分线、两圆的公切线、圆的切线、三角形的内切圆、比例线段等等。《代形合参》（1894年）中第二章以及附卷涉及几何作图。近年发现一部收集几何作图题的译著《几何画法》，不见各算学书目，简介如下。该书由“英国费士特纂，顺德黄桂芬达旨”，光绪丙午（1906年）浮鸥馆刊本，由湖北学务处鉴定。该书不分卷，共收集116 个几何作图题，严格遵循尺规作图规则。

在实际作图中，人们往往不遵守严格的尺规作图规定，所用作图方法大体有三类：尺规作图、不完全尺规作图以及机械作图（如《灵台仪象志》中运用椭圆规作椭圆）。

尺规作图方法传入中国后，有清一代二三百年间，中算家对其作图理论、规则、效用范围等研究不多。李善兰的《椭圆拾遗》卷二涉及9 个圆锥曲线焦点作图，可为中算家对尺规作图研究的代表，这些为本小节讨论的主要内容。

《椭圆拾遗》卷二共9 款，讨论9 个求焦点位置的作图问题，这些问题均为已知椭圆的一个焦点及其他一些条件，用尺规作图（或不完全尺规作图）的方法求作另一个焦点。冯立昇、牛亚华首次关注了李善兰这一成就，并以其中3 题为例对李氏作图理论进行了探讨。本文注意到李氏在每个作图之后均简要讨论了已知曲线为抛物线和双曲线的情形，因此实际上李氏给出了已知圆锥曲线的一个焦点及其他一些条件，用尺规作图的方法求作另一个焦点的问题，并给出了证明。解决这类问题需要综合应用圆锥曲线及其切线的性质以及几何作图方面的知识。应该说，李善兰是研究圆锥曲线作图问题的第一位中算家。^[8]下面对其主要几个作图题进行讨论。

（Ⅰ）有一心（F1），有最卑点（距F1 最近的点A），有椭圆周一点（P），求余一心（F2）。

李氏的作法是，如图4-2-6，联结A F1 （卑径）和P F1 （距心线），并过P 作PD⊥A F1 的延长线于D，AD 为椭圆矢。李氏根据卷一第14 款的结论得到比例式

由此可以作出2c，这样F2 就确定了。

图4-2-6

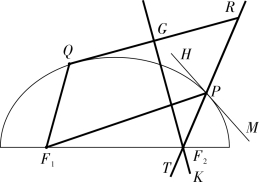
图4-2-7

同时，李氏指出“若卑径较与矢相等，则为抛物线；卑径较大于矢，则为双曲线”，即如果卑径较（PF1-AF1）与矢（AD）相等，即PF1-AF1=AD，则表明原曲线为抛物线；若PF1-AF1＞AD，则表明原曲线为双曲线。此即表明李氏实际给出了已知任一圆锥曲线的一焦点、一卑点和其他任一点，求作另一焦点的作法。

（Ⅱ）有一心（F1），有椭圆周二点（P，Q），其一点（P）并知切线（H M），求余一心（F2）。

李氏的作法如下，如图4-2-7：

（1）联结F1Q，F1P，作线段PT，使得∠QPT=∠HPF1。

（2）反向延长PT，取一点R，使得PR=F1P-F1Q。

（3）联结QR，作QR 的中垂线GK 交PT 于点F2，即为所求。

在证明之后李氏指出“若午未丙线与乙寅平行，则为抛物线；若交点丙在切线之外，则为双曲线”，即若GK∥RT，则已知曲线为抛物线，则如图4-2-8左图所示。若F2 与F1 在切线HM 的两侧，则已知曲线为双曲线。即给出已知双曲线上两点和过其中一点的切线，求作双曲线的另一焦点。根据李氏提示作图，如图4-2-8右图所示，不过此时PR=F1P+F1Q。

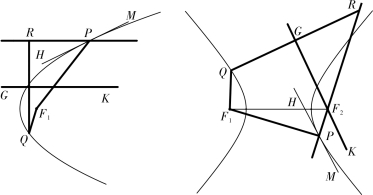
图4-2-8

（Ⅲ）有一心（F1），有椭圆周三点（P1，P2，P3），求余一心（F2）。

图4-2-9

李氏的做法如下，如图4-2-9：

（1）联 结F1P1，F1P2，F1P3 （不 妨 设F1P1＜F1P2＜F1P3），在F1P2 及其延长线上取点M，N，使得F1M=F1P1，F1N=。

（2）联结P1M，过N 作NH ∥PM 交P1P2 的延长线于H 点。联结P3H，过F1 作F1K3⊥H P3 于K3 点。过P2 作P2K2∥P3K3于K2 点。

（3）在F1 P3 上取一点D，使得。在过F1 点与F1 K3的垂线上取点S，使得F1S=F1D。

（4）在F1 K3 的反向延长线上取点A，使得，即F1A=a-c（卑径）。

（5）利用比例式作出2c （倍心差），在F1K 上取点F2使得F1F2=2c，F2 即为所求。

证明：由卷一第14 款，（k 为卑径=a-c，i=1，2，3）

由合比、分比定理，(www.daowen.com)

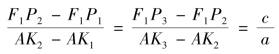
所以

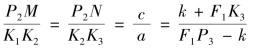
李善兰指出，若K2K3=P2N，则表明原曲线为抛物线；若K2K3＜P2N，则表明原曲线为双曲线。

（Ⅳ）有一心（F1），有最卑点（A），有椭圆的一切线（l），不知切点，求余一心。

李善兰《椭圆拾遗》（卷二）第二十五款（续修四库全书本）

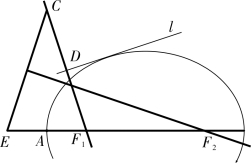
图4-2-10

如图4-2-10，最卑点A 为距F1 最近的一点，即椭圆的长轴的一端点。过F1 作切线l 的垂线交l 于D 点，取DC=DF1，反向延长AF1，取AE=AF1，联结CE，作CE 的中垂线GH 交A F1 的延长线于F2 点，即为所求。

若GH∥AF1，则原曲线为抛物线；若GH 与AF1 交点在切线l 另一侧，则原曲线为双曲线。即已知双曲线的一焦点与相对应的顶点和一不知切点的切线，求作双曲线的另一焦点。

（Ⅴ）有一心（F1），椭圆周三切线（l1，l2，l3）俱不知切点，求余一心（F2）。

如图4-2-11，过F1 分别作l1，l2，l3 的垂线段F1P1，F1P2，F1P3，使得l1，l2，l3 分别是F1P1，F1P2，F1P3 的中垂线，联结P1P2，P2P3，分别作P1P2，P2P3 的中垂线MM′，NN′，它的交点F2 即为所求。

（Ⅵ）有一心（F1），有椭圆周一点（P），有二切线（l1，l2），俱不知切点，求余一心（F2）。

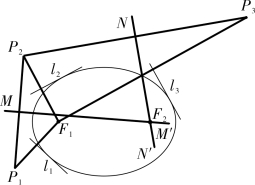
图4-2-11

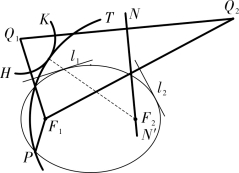
图4-2-12

如图4-2-12：

（1）分别取两点Q1，Q2，使得li 垂直平分F1Qi（i=1，2）。

（2）联结Q1Q2，作Q1Q2 的中垂线NN′。

（3）以Q1 为圆心、F1P 为半径作圆弧，在NN′上取一点F2，使得以F2为圆心、F2P 为半径的圆弧与相切，则F2 为所求。

（Ⅶ）有一心（F1），有椭圆周二点（P，Q），有一切线（l），不知切点，求余一心（F2）。

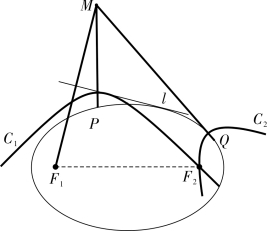
图4-2-13

如图4-2-13：

（1）作点M，使得l 垂直平分F1M。

（2）以P，M 为焦点，PM 为实轴，PF1 为虚轴长作双曲线C1。

（3）以Q，P1 为焦点，QM 为实轴，QF1 为虚轴长作双曲线C2，则两曲线C1，C2 的交点F2 即为所求。

若双曲线C1，C2 没有交点，则原曲线为抛物线；若交点与F1 分在切线的两侧，则原曲线为双曲线。

从李氏作图可以看出，主要利用圆锥曲线向径与轴之间的关系以及切线性质进行作图。值得注意的是，在第（Ⅵ）中用到作一圆弧与另一圆弧相切和第（Ⅶ）中利用两条双曲线来确定点，这些并没有遵守严格的尺规作图限制。第（Ⅶ）作法实际就是“由三个已知点向第四个未知点作三条线段使其差为已知”。1593年，比利时数学家罗曼努斯 （A.Romanus，1561—1615年）在企图解阿波罗尼问题时也涉及这个问题，当时他也是用两双曲线交点来确定点，但同时代的数学家并不满意。^[9]直到1687年，牛顿在讨论圆锥曲线轨道运动问题时（《自然哲学之数学原理》卷1，第4 章，引理16）^[10]遇到同样的问题，他沿着罗曼努斯的思路，用尺规作图方法作出第四点。这应该是西方数学家恪守尺规作图限制的结果。而从李善兰的作图可以看出，他运用双曲线相交来确定点的作法很自然，表明欧氏几何尺规作图传入中国时所内含的作图规则并没有完全进入中算家的内心。