通过第二章的论述可知，在椭圆轨道问题推算中，椭圆向径与实行角之间的关系很重要，这个关系实际上就是现在的椭圆的极坐标方程。李善兰的《椭圆拾遗》卷一第13—20 款，通过几何推算得到了相当于椭圆极坐标方程的关系。他先给出几个预备定理。

第13 款：“大小二径较比如大小二矢比”。

如图4-2-4，卑径F1A=F2B=a-c，F1P，F2P（＜F1P）为椭圆两条共点焦半径，PQ⊥AB 于Q，称AQ 为大矢，称BQ 为小矢，作F1M=F2N=F1A，则PM=F1P-F1M，PN=F2P-F2N，他们分别称为大小二径较。该款结论为：

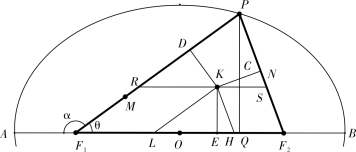
图4-2-4

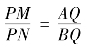
李善兰的证法为：

作△F1PF2 的内心K，K 到三边的距离分别为KC，KD，KE，过K 作KH∥PF2，KL∥F1P，RS∥F1F2，则有F1D=F1E，PD=PC，F2C=F2E

由椭圆的性质有

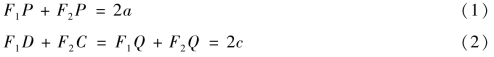
由（1）-（2）得

(F1P-F1D)+(F2P-F2C)=2(a-c)=PD+PC=2PD=2PC

F1M=PD=F2N=PC=a-c

F1P=F1D+DP=F1P+(a-c)=AE；

同理可得F2P=BE。

由ΔKCS ≌ΔKEH，ΔKDR ≌ΔKEL 得到

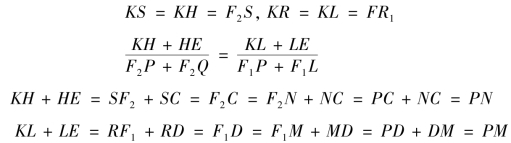
由比例性质有

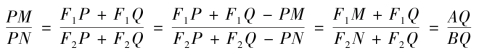(www.daowen.com)

在此款中，△F1PF2 现称为焦点三角形，证明中E 点很重要，它把长轴分成两部分，刚好与两焦半径对应相等，即AE=F1P，BE=F2P。而E 点恰好就是△F1PF2 内心K 在长轴上的投影。根据上面的证明，这一款的结论可以写成

Q 点是P 点在长轴的投影，F1E+F2E=2c，AQ+BQ=2a，此式具有很奇妙的对称性，这种对称性凸现出李善兰的几何功底。

第14 款：“径较与矢比恒如倍心差（2c）与长径（2a）比”。如前图4-2-4，

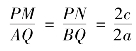
第15 款：“心垂线（KE）与正弦（PQ）比恒如两心差与高径比”，即。

第16 款：“任取交径（F1P）之一为距心线。距心线为一率，卑径较[F1P-（a-c）] 为二率，卑径为三率，得四率为矢率。高径为一率，倍心差为二率，卑径为三率，得四率为径率。矢率与径率比恒如实引矢与全径比”。

由定义，矢率=，径率=，令F1P=r，根据第13—15 款的结论可以得到

即

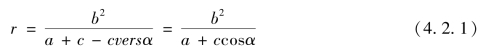
该款李氏给出向径r 与“最卑后”实行角（实引角）α 的关系。如图4-2-5，若以F1 为极点，为正方向，r （=F1P）为极径建立极坐标系，则式（4.2.1）为椭圆的极坐标方程，其中α=∠AF1P。

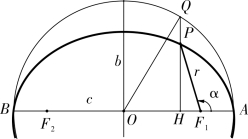
图4-2-5

第19 款在前两款的基础上得到椭圆向径r 与“最高后”实行角（实引角）θ 的关系式

此式可以看成以F1 为极点，为正方向，r （=F1P）为极径的极坐标系下的椭圆极坐标方程，其中θ=∠BF1P（如图4-2-5）。

至此，李氏实际上运用综合几何的方法得到了椭圆的两个极坐标方程[式（4.2.1）与式（4.2.2）]，这两个关系是椭圆轨道问题的本质关系，也是之后《椭圆拾遗》卷三利用级数处理椭圆轨道问题的基础。