《椭圆拾遗》卷一由第1—20 款组成给出20 个命题，绝大多数是李善兰独立提出并给予证明的。

命题1 和命题2 利用投影的概念证明椭圆基本定理：“椭圆与辅圆对应弦之比，等于椭圆长短轴之比”。对于椭圆与大辅圆的关系：“盖平圆侧视之即成椭圆，平圆诸正弦恒为弦，侧视所成椭圆诸正弦恒为勾，成无数等势勾股形，故比例恒同也”。对于椭圆与小辅圆的关系：“盖椭圆从长径端侧视之，长径必稍短，渐侧渐短与短径等，即成平圆矣，椭圆诸正弦恒为弦，侧视所成平圆诸正弦恒为勾，成无数等势勾股形，故比例恒同也”。在这里，李善兰把椭圆看作大辅圆的投影，而小辅圆则是椭圆的投影。

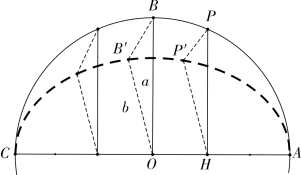
图4-2-1

如图4-2-1，设ABC 为给定圆，O 为圆心，OA，OB 互为垂直径，椭圆AB′C 为圆的投影，OB′为OB 的射影，P 为圆上任意一点，P′ 为其在椭 圆 上 的 射 影，显 然 RtΔOB′B∽RtΔHP′P，故

OB：OB′=HP：HP′=a：b

同理可证明椭圆与小辅圆之比例式也成立。

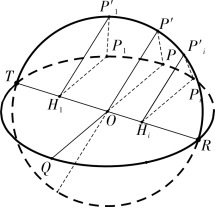
命题3 是：“凡椭圆斜交斜径之正弦与斜径上平圆之正弦比，恒如半属径与半斜径比”。如图4-2-2，RPTQ 为椭圆，RT，PQ 为椭圆上一对共轭直径，RP′TQ′为以RT 为直径的圆，即“斜径上平圆”，Hi 为椭圆斜径RT 上任一点，HiPi ∥PQ，HiPi 为椭圆相对于直径RT 的“正弦”。OP′ ⊥PT，HiPi′ ⊥PT，HiPi′为圆相对直径RT 的正弦。系列三角形ΔHiPiPi′相互相似，此命题的结论为：

(www.daowen.com)

图4-2-2

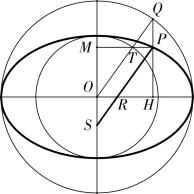
图4-2-3

李善兰也采用了投影的方法证明了这个命题，他说：

试置椭圆柱自短径端斜截之，令成平圆面，复自长径端斜截之，仍为椭圆面，令二面之交线过柱心，则交线即斜径，二面正弦与圆柱周诸直线成无数等势三角形，故比例恒同也。

可以看出，若椭圆已知的一对共轭直径为长轴和短轴，则此命题即为椭圆基本定理，因此它实质上是推广的椭圆基本定理。利用这个定理，李善兰又推出了一些新的结果，主要是大小辅圆与椭圆面积的关系，以及以共轭直径为边的椭圆的外切平行四边与椭圆的面积关系。

命题12 讨论椭圆规的原理：“任自椭圆周一点作线至长径上，令等于小半径，则引长之至短径，必等于大半径”。如图4-2-3，设P 为椭圆上任意一点，从P 点引直线交至长轴于R 点使PR=b，延长PR 交短轴于S 点，则有PS=a。

李善兰利用椭圆基本定理证明了这个原理。如图4-2-3，作椭圆的大、小辅圆，过P 点作椭圆正弦PH，余弦PM，分别交大辅圆于Q 点，交小辅圆于T 点。由基本定理有，所以，所以RtΔOHQ ∽RtΔOMT，所以点T 在OQ 上。又PR=b=OT，可证PR ∥OT，又PQ ∥OS，所以PS=OQ=a。

李善兰明确指出：“用十字槽作椭圆周即此款之理也。”十字槽指的是椭圆规，南怀仁的《灵台仪象志》（1674年）中有图示（见本书图1-2-1），但没有说明构造原理。