在《致曲图解》第四节“论诸曲线式皆有规线”中给出了规线的概念。规线不见于夏氏之前的中文论述，现代数学词汇中无相应术语。先看看夏氏是怎样定义规线的。

如图4-1-3（1）— （4）中，以AB （夏氏称之为“长径”=2a）、AC（夏氏称之为“起首规线”=通径=）为两直角边，斜边CB （或延长线）上任一点Q 到AB 的垂线段QR 就是该垂线段与曲线的交点P 所对应的规线。即对于圆锥曲线上任一点P 来说，在CB、AB 上分别有一点Q、R 与之对应，AR 为横线，PR 为直线，规线为QR。根据定义，横线、直线、规线为连比例三率，即PR2=AR×QR。其中特殊的，通径为长径与短径的连比例末率。

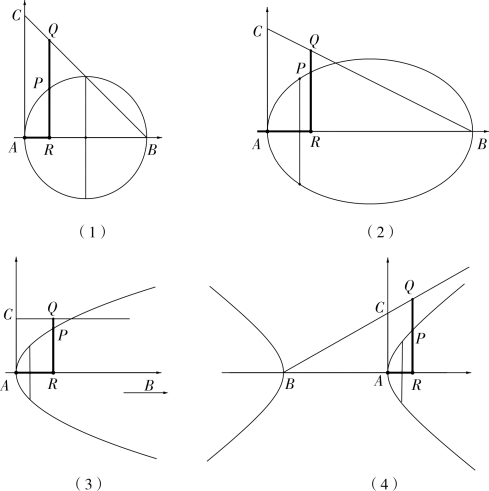
图4-1-3

显然，圆与椭圆的情形比较好解释。对于抛物线，紧承“广义准线”中的观点，如图4-1-3（3），B 点在无穷远点，CB 势与AB 平行，这时规线就为一常量，恒等于“起首规线”即通径，这样

PR2=QR×AR=通径×AR

这刚好是抛物线的标准方程。

对于双曲线，它是椭圆的反式，规线的作法相同，不过方向相反，横线越大，规线也越大，此时点Q 在BC 的延长线上。

在开篇夏氏这样描绘规线：(www.daowen.com)

凡诸曲线式之横直线皆以规线为权衡……凡起首规线曰通径。平圆、椭圆、抛物线、双曲线四式俱以规线乘横线为直线自乘方。

结合具体的作法，规线具有明显的解析几何意义，在这里它起着建立代数方程的作用，但夏氏在此并没有使用坐标系。更进一步，如果我们以A 为原点，AB，AC 所在的射线为横、纵两轴，则四曲线的方程可以统一写成

y2=x×规线

刘钝先生对“规线”的来源没作进一步的探讨。本书认为，规线的提出与《代微积拾级》卷八的内容有关。《代微积拾级》卷八“诸曲线依代数式分类”第二款论述了经过一定的坐标变换，可以得到二次曲线的一个比较简洁的统一方程

此时坐标系就是依图4-1-3建立，其中A 为原点，为x 轴，为y轴。曲线为圆时，对应着p=2，q=-1；曲线为椭圆时，对应着p=，q=；曲线为抛物线时，对应着p=2a，q=0；曲线为双曲线时，对应着。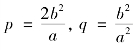

《致曲图解》全书的思想就是想从几何的角度对圆锥曲线进行统一的描绘，规线显然是（p+qx）的几何解释，而整个第四节可以看成是对式（4.1.1）进行的几何解读。

相应的，第9 节“论诸曲线式之斜规线”则是第4 节“正规线”的拓广，实际上就是斜坐标系中二次曲线统一方程的几何解释，在此不再赘述。