《致曲图解》第1 节“论诸曲线始于一点”开篇就从平面截圆锥面得到各种圆锥曲线的实事上着手，夏氏认为：

诸曲线之形始于一点，变点而成线，线渐阔而成大小径渐等。诸椭圆至大小径等而成平圆。又变而为大小径渐不等，椭圆至大小径不等之极，而成抛物线，又渐而成双曲线，以至无数双曲线。愈截至边则形愈狭，狭之至而复成一点。故点也，线也，平圆也，椭圆也，抛物线也，双曲线也。形不同而得形之原无不同也。原者何？一点也。数于何生？生于圆锥。

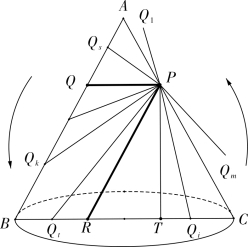
图4-1-1

如图4-1-1，夏氏相当于用过圆锥面上一点P 的半平面去截圆锥面，只考虑半平面与圆锥面两条母线及底面直径所组成的三角形ΔABC 的截线。设半平面以逆时针方向去截圆锥面，当截线为PQ1 点时，交于一点P，故说“始于一点”；当截线与AC重合时，则截线为线AC，当截线在PA 与PR （PR∥AB）之间时，得到椭圆，中间截线有一特殊位置，即平行于底面的PQ 时，得到椭圆的特殊形式即平圆；当截线到达极限位置PR 时，则得到抛物线；当截线在PR 与PC 之间时，得到双曲线；到达PC 时，得到线PC；之后，又归于点P。当截面连续变化时，几何图形能从一种形状连续变化到另一种形状，可以看出夏氏以一种运动的、连续变化的观点去考察圆锥截线。这种思想与开普勒提出的通过焦点的移动来转换圆锥曲线的思想类似。进而，夏氏得到了4 个命题：

命题1：椭圆至大小径等而成平圆；

命题2：抛物线为椭圆和双曲线之极式；

命题3：椭圆和双曲线互为反式；

命题4：平圆与正交双曲线互为反式。

这4 个命题表明4 种曲线之间的关系。由此，他得到研究圆锥曲线的综合方法：首先研究最为简单的圆的有关性质；其次由命题1 把圆的性质类推到椭圆上；再分别利用命题2 和命题3，通过极式和反式得到抛物线和双曲线的相应性质。命题4 是命题3 的特例，是夏氏研究双曲函数的理论基础。^[2]夏氏就是运用这种思想独创出圆锥曲线的“广义准线”。下面进行详细论述。

准线是当今数学圆锥曲线统一定义的基础概念，而在《代微积拾级》中仅仅提到抛物线的准线，卷五“论抛物线”开篇说：

设一定点，一直线，抛物线之每点距定点与距直线恒等。定点即抛物线之心，直线名曰准线。

在《致曲图解》第三节“论诸曲线式皆有准线”中，夏氏论道：“凡曲线上任一点抵心（焦点）与抵准线之二线必相等。”从后文的论述看，这一定义只有在抛物线的情况下与《代微积拾级》的含义相同，不妨采用刘钝先生的命名称之为广义准线。

圆的情形最简单的一种情况是，它的准线是倍径的同心圆。如图4-1-2（1）恒有PiAi=AiF1。

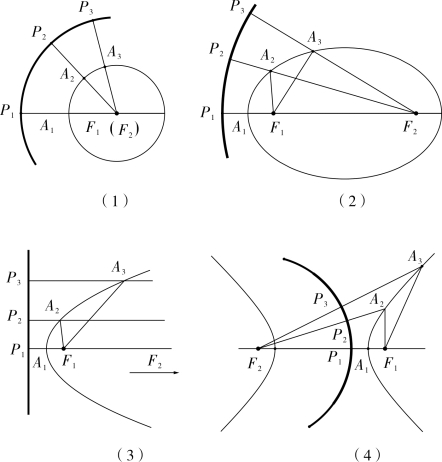
图4-1-2

由圆到椭圆，是特殊到一般的过程，原来重合在一起的两个焦点F1，F2分开了，但准线还保持其基本特征，由此得到椭圆准线的作法。如图4-1-2（2），以F2 为圆心，以F2P1=2a （实轴）为半径作一个圆，由椭圆的性质可以得到对该圆上的任一点Pi，均有PiAi=AiF1，因此所作的圆就是椭圆的一条准线，同理，可以得到另一条以F1 为的圆心的准线。

当F2 向右移动时，椭圆在长轴的方向上开始被“压扁”，一旦F2 到达无穷远，椭圆就变成它的极式即抛物线，图4-1-2（2）即成为图4-1-2（3）。夏氏说：

抛物线为椭圆之极式，则只有左心，其右心（F2）远在不可穷极之外，则室胃、胃奎、虚壁诸线（PiF2）势不能到右心。右心既不能到，则此诸线不能为半径，而不得不为轴平行之横线矣。又依前图[图4-1-2（2）] 之例，以右心为心作一式外平圆，而抛物线右心远在不可穷极之外，则平圆半径之大为无量大；而前图壬木线（）亦为无量大。夫一段弧线若大至无量必至变弧线为直线，此抛物线之准线所以不为弧线而为直线也。

这就是说，抛物线的准线是一条直线P1P2，它上面任一点Pi 满足PiAi=。

在这里，夏氏从逻辑上很自然地引入两个非同寻常的观念：首先他认为一组平行线有一个公共的无穷远点，其次他把直线看成直径为无穷大的圆。这俨然已经是近代射影几何中的命题了。(www.daowen.com)

根据命题2，图上处于无穷远处的F2 如果继续向“右”移动，那么可以设想它将出现于左端的无穷远处，与之相应的图形是一个开口相反的抛物线；如果F2 继续向右移动，相应的图形就是椭圆的反式双曲线了。

至于双曲线的准线，可以仿照椭圆准线的作法，如图4-1-2（4），以F2 为圆心，F2P1=2a （实轴）为半径的圆就是双曲线的一条准线，同理，可以作出另一条以F1 为圆心的准线。

值得注意的是，在图4-1-2（1）至（4）的变化中，其实暗含着一种连续变化的思想：圆锥曲线从其中的一个连续变为另一个时，只需考虑焦点的各种移动方式。如椭圆有左右两个焦点F1，F2，若固定F1，考虑F2 的移动。当F2 向左移动时，椭圆逐渐趋向于圆，F2 与F1 重合时便是圆；当F2 向右移动时，椭圆逐渐趋向于抛物线，F2 到无穷远处便是抛物线；当F2 从无穷远处由左边回到圆锥曲线的轴上时，便为双曲线。这与开普勒的看法可以说是一致的。这就是夏氏所谓的：

椭圆利用聚，抛物线利用远，双曲线利用散，其理皆出于平圆。

当某个几何图形从一种形状连续地变为另一种形状时，如果某些几何特征仍保持不变，那么通过第一种形状的性质可以类比得到第二种形状的性质，反之亦然。这就是近代几何中的连续性原理。可以看出夏氏“广义准线”恰好是这种思想的体现。

后来杨兆鋆在其《须曼精庐算学》^[3]卷二“抛摆致用”第六题说：

西人言抛物线有准线而不及他曲线，近来天算家言椭圆双曲线皆有准线，但不为直线而为圆线。

此说显然源于夏鸾翔。

夏鸾翔《致曲图解》的“总论”以及第三节“论诸曲线式皆有准线”中一页（此为夏氏手稿影印，续修四库全书本）

项氏还将这种思想运用于对圆直径的推广上。

他说：“平圆有相等二径，椭圆、双曲线皆有大小二径。若椭圆大径至无穷、两心差远至无穷则成抛物线式；双曲线大径大至无穷、两心差远至无穷亦成抛物线式。”又说，“双线者椭圆之反式……椭圆二径在形内、双线二径在形外。”在此将直径由封闭图形推广到开放图形。

紧接着他又将这种思想运用到直径与共轭直径的推广上。

他说：“凡诸曲线式有正径、有兑径。正径有二，兑径亦有二……诸式内与小兑径平行诸线必平分于大兑径上，与大兑径平行诸线必平分于小兑径上。”兑径即广义的直径，后一句相当于给出广义直径的定义和共轭直径的作法。这就完成了对直径与共轭直径关系上的拓广。

《代微积拾级》对这一概念也作了些介绍：“凡二斜径，此径与彼径端之切线平行，彼径必与此径端之切线平行，名曰相属径。”夏氏的说法则与广义直径的现代定义相同，即把直径看成一簇平行弦中点的轨迹，只不过他预先假定了这条轨迹是直线段。

对于直径与广义直径的关系，夏氏还得到了《代微积拾级》中所没有的几个关系：

（椭圆）两兑径和之最大者为相等二兑径和，最小者为两正径和；

（双曲线）两兑径和之最大者为无穷数，最小者为两正径和；

双线之相等二兑径即渐近线也。