陈平瑛，字修常，号仲容，福建侯官人，生于1879年^[88]，卒年不详。陈氏于1897年参加福建省丁酉科乡试得中，名列第75 名，时年仅17 岁，为世人所称道。时人称他“生而颖悟，幼通算理，年未弱冠，以算学名天下，其丁酉科闱中所对天算策问，传颂于时”^[89]。陈平瑛曾为黄启明（字佩星）的《微积通诠》一书写过序，此序中提及“岁甲辰（1904年），余课算于广州府中学堂，花县黄君佩星惠然造访，谈论数理，彼此甚欢”^[90]。可知，陈平瑛曾在广州府中学堂做过算学教习。其兄陈修龄，号伯达，对算学也有研究，有《公式演算》五卷（1905年）传世。

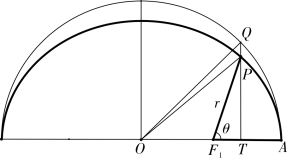
图3-5-3

陈平瑛所著《中西算学题镜》（八卷，1901年）卷七“曲线微积”专论二次曲线求积问题。在此仅就第六题对椭圆向径扫过面积的求法为例进行分析。原题为“设曲线为椭圆，求其自心所截之面积”。如图3-5-3，已知∠AF1P=θ，求SAF1P。

陈氏采用微积分方法求解，大概如下：

依据《代微积拾级》卷六第十六款，以椭圆焦点为极点，长半轴为极径，椭圆的极坐标方程为

其中p=是半通径，r 为带径（焦半径），θ 为极轴到焦半径的角。椭圆向径扫过面积AF1P 的面积微分为

由《微积溯源》第70 款有

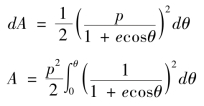
令1+ecosθ=x，则dx=-esinθdθ，所以

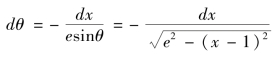
则

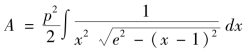
令e2-1=-k，由《微积溯源》第128 款有

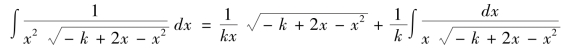
又由《微积溯源》第129 款和第126 款有

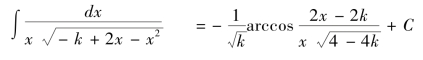
所以

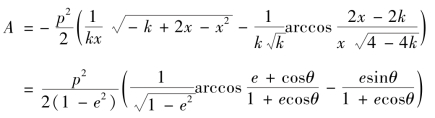
即

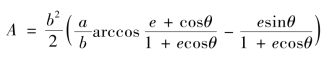
如果不考虑当时所用的符号，陈氏所用方法与现今无异。

另外，黄启明在其《微积通诠》（1905年陈平瑛序）第十四卷中称：

新法日躔数理设实引求平引之面积、求实引面之面积，皆以椭圆立算，而辗转推求，布算繁重，且以角求积则易，以积求角则难。李壬叔推得之式，学者仍苦其繁。兹从极曲线微分之公式演成有实引求平引之公式及平引求实引之公式如左。^[91]

黄氏当时为广西浔州府中学堂数学教习，他的推算过程与陈氏差不多，都是从椭圆的极坐标方程入手求椭圆向径扫过的面积。显然，二人的计算过程自然比李善兰的级数回求术要简洁得多。

从张氏、孙氏、沈氏、陈氏、黄氏等人的论述中可以看出，他们对微积分的运用已达到很熟练和自然了。^[92]

本章论述中算家运用解析法对圆锥曲线研究的代表成果。如果说董祐诚对椭圆周长的认识还停留在表面上的话，项名达的椭圆求周术则已深入到椭圆周长的本质，他利用椭圆基本定理将割圆术运用到椭圆上，依据自己对平方根展开式的研究以及大量的运算技巧，得到椭圆周长的级数解析式。夏鸾翔由于吸收了《代微积拾级》中的积分术得到了较之其师更为一般的成果，这是他超越项氏之处。可是他囿于自身的知识结构，守住“递加数”不放，于《代微积拾级》中的级数代数表示法和微分术不顾，其所得成果显得很笨拙，也不利于《代微积拾级》中微积分知识的传播。李善兰抓住椭圆轨道问题的实质关系，运用级数的方法给出了开普勒方程的级数解，较之以前的研究，李氏成果层次更高，认识也更为深刻。较之夏鸾翔，李氏吸收了《代微积拾级》中的级数的代数表示法。可他得到级数展开式的方法依然承续董氏将级数系数与传统垛积术联系的方法，而并没有吸收《代微积拾级》中建立曲线方程之后运用泰勒展式建立级数的更为一般有效的方法。

张燨、孙祝耆、沈保枢、陈平瑛等这些有着新式学堂学习经历的人相较于夏鸾翔、李善兰，数学水平并不如他们的前辈，但他们在求积问题上能订正后者的错误，改进后者的方法，这中间最重要的原因是他们相较于前辈，经过圆锥曲线知识的教学、普及以及微积分在夏、李之后的华蘅芳等人的解读，他们的知识结构已经发生很大的改变，微积分知识于他们已不是什么艰深的知识，很大程度上已经是他们知识构成的一部分了，所以运用也比较自如了。

【注释】

[1]李迪：《中国数学通史·明清卷》，南京：江苏教育出版社2004年版，第269 页。

[2]李迪：《中国数学通史·明清卷》，南京：江苏教育出版社2004年版，第190、276 页。

[3]李兆华：《董祐诚垛积术与割圆术述评》，吴文俊主编：《中国数学史论文集》第三集，济南：山东教育出版社1987年版。

[4]李迪：《中国数学通史·明清卷》，南京：江苏教育出版社2004年版，第387 页。

[5]李兆华：《李善兰垛积术与尖锥术略论》，《西北大学学报》（自然科学版）1986年第4 期。

[6]李兆华：《戴煦关于对数研究的贡献》，《自然科学史研究》1985年第4 期。

[7]华里司原著，傅兰雅、华蘅芳合译：《微积溯源·华蘅芳序》，江南制造局本，1874年。

[8]Loomis，E.Elements of Analytical Geometry and of the Differential and Integral Calculus.New York：Harper & Brothers，1852，p.115.

[9]陆晓明、王能超：《泰勒公式通古今：微积分史学习札记之二》，《高等数学研究》1998年第3 期，第14 页。

[10]华蘅芳：《微积溯源·序》，傅兰雅、华蘅芳合译：《微积溯源》，江南制造局本，1873年。

[11]黄启明：《微积通诠·凡例》，菁华阁刊本，出版时间不详，有陈平瑛1905年序。

[12]朱学贤：《泰勒》，吴文俊主编，《世界著名科学家传记·数学家·III》，北京：科学出版社1994年版，第282-289 页。

[13]（美）莫里斯·克莱因著，朱学贤、申又枨、叶其孝等译：《古今数学思想》第二册，上海科学技术出版社2002年版，第26 页。

[14]（美）维克多·J.卡兹著，李文林、邹建成、胥鸣伟译：《数学史通论》（第2版），北京：高等教育出版社2004年版，第456 页。

[15]杨冰：《南菁文钞·微积术补代数未尽说》，高时良、黄仁贤主编：《中国近代教育史资料汇编·洋务运动时期教育》，上海教育出版社2007年版，第839 页。

[16]（美）罗密士著，（英）伟烈亚力译，（清）李善兰述：《代微积拾级》，伟烈亚力序，墨海书馆刊行，咸丰己未（1859年）。

[17]同上，李善兰序。

[18]华蘅芳：《学算笔谈·卷五·论加减乘除开方之用》，行素轩算稿本，光绪癸巳（1893年）。

[19]中华书局编辑部编：《王韬日记》（增订本），汤志钧、陈正青校订，北京：中华书局2015年版，第285 页。

[20]罗士琳：《畴人传续编·董祐诚》，林文照主编：《中国科学技术典籍通汇·综合卷》第七册，郑州：河南教育出版社1993年版，第599 页。

[21]（清）项名达：《椭周术》，杨尚文：《连筠簃丛书》，道光廿八年（1848年）灵石杨氏刊本。以前关于项氏的研究均不及此条。

[22]诸可宝《畴人传三编》卷四“戴煦”传后附记：“闵杨宝臣，字湘云，笃嗜数学。道光二十五年（1845年）夏，介项学正见先生，有‘愿天生圣人以正天算之语’。他行事未详。”又，《皇清书史》卷十四称：“杨宝臣，号湘云，侯官人，官道员，能擘窠大书，杨雪沧有诗咏之。”又，莫友芝咸丰九年十二月十八日给九弟莫祥芝的家信中称：“前数月来，颇识得海内才人不少。王子怀侍郎（老成练达，有守有为），名茂荫；尹杏农侍御，名耕云（敢言之士）；杨缃芸户郎，名宝臣（长于天文，曾面斥权人罪），皆有识有为，并不得安于其职，或疾或降。”（第三条转引自张剑：《莫友芝人生及学术成就谫论》，《中国政法大学学报》2015年第2 期，第139 页）莫友芝曾为李善兰的《则古昔斋算学》署检。“缃芸”与“湘云”为同一人。

[23]李俨：《中算家的圆锥曲线说》，《李俨钱宝琮科学史全集》第七卷，沈阳：辽宁教育出版社1998年版，第491-514 页。

[24]何绍庚：《椭圆求周术释义》，《科学史集刊》第11 期，北京：地质出版社1984年版，第130-142 页。

[25]牛亚华：《项名达的椭圆求周术研究》，《内蒙古师范大学学报》（自然科学版）1990年第3 期，第53-64 页。

[26]何绍庚：《椭圆求周术释义》，《科学史集刊》第11 期，北京：地质出版社1984年版，第130-142 页。

[27]钱宝琮：《中国数学史》，北京：科学出版社1981年版，第332-333 页。

[28]李迪：《中国数学史简编》，沈阳：辽宁教育出版社1984年版，第381 页。

[29]刘长春：《夏鸾翔在椭圆计算上的若干贡献》，《内蒙古师范大学学报》（自然科学版）1986年第2 期，第35-42 页。

[30]宋华：《夏鸾翔对微积分的学习与使用——〈万象一原〉内容分析》，内蒙古师范大学硕士学位论文，2003年。

[31]郭世荣：《清末数学家的微积分水平》，《第二届中国少数民族科技史国际会议论文集》，北京：社会科学文献出版社1996年版。(www.daowen.com)

[32]李兆华：《晚清算学课艺考察》，《自然科学史研究》2006年第4 期。

[33]刘洁民：《晚清著名数学家夏鸾翔》，《中国科技史料》1986年第4 期。

[34]刘洁民：《关于夏鸾翔的家世及生平》，《中国科技史料》1990年第4 期，第47 页。

[35]此即现行《致曲术》与《致曲图解》两种。据《致曲术》和《致曲图解》稿本，此两种原为一书上下卷，题称《致曲》。华世芳的《近代畴人著述记》称：“杭州夏紫笙鸾翔遗书凡四种，曰《万象一原》《致曲术图解》，……曰《洞方术》，……曰《少广缒凿》。”见（清）华世芳：《近代畴人著述记》，华蘅芳：《学算笔谈》，行素轩算稿本，光绪癸巳（1893年）。同时考虑到“致曲”两种体例与《洞方术图解》（2 卷，卷一为“演术”，卷二为“图解”）一致，称之为《致曲术图解》（二卷）更接近夏氏本意。

[36]（清）夏鸾翔：《致曲术》，戴念祖主编：《中国科学技术典籍通汇·物理卷》第1册，郑州：河南教育出版社1993年版，第1118-1129 页。

[37]（清）夏鸾翔：《万象一原·自序》，振绮堂丛书本，同治元年（1862年）。

[38]（清）徐异：《万象一原校勘记》，沿沂亭算稿，光绪辛丑（1901年）。

[39]斜双曲线，相对“正双线”（等轴双曲线）而言，即一般双曲线。

[40]（清）夏鸾翔：《致曲术》，戴念祖主编：《中国科学技术典籍通汇·物理卷》第1册，郑州：河南教育出版社1993年版，第1125 页。

[41]实际上，《致曲术》中注语“半心差幂乘半径幂除又余弦幂乘半径幂除”中“余弦”应作“正弦”，正弦不一定大于半径。

[42]（清）项名达：《象数一原》，卷六，上海刻本，光绪戊子（1903年），第7 页。

[43]在《万象一原》中夏鸾翔在处理对数螺线求积问题时用到lnx 的展开式。

[44]（清）夏鸾翔：《洞方术图解》，戴念祖主编：《中国科学技术典籍通汇·物理卷》第1 册，郑州：河南教育出版社1993年版，第1103 页。

[45]（清）夏鸾翔：《洞方术图解·自序》，戴念祖主编：《中国科学技术典籍通汇·物理卷》第1 册，郑州：河南教育出版社1993年版，第1093 页。

[46]李兆华：《招差术略论》，李兆华：《古算今论（第二版）》，天津科技翻译出版公司2011年版，第288 页。

[47]邹伯奇：《刻夏紫笙算书遗稿序》。

[48]（清）华蘅芳：《学算笔谈》，卷十二，行素轩算稿本，光绪癸巳（1893年）。

[49]华氏《学算笔谈》共12 卷，前六卷在1882年写成后先刊刻。后六卷陆续写成后才成12 卷，于1893年在武昌刊刻。见华蘅芳：《行素轩算稿·学算笔谈·卷六跋》，光绪八年（1882年）梁溪华氏刊本。

[50]高红成：《夏鸾翔对二次曲线求积问题的研究——兼论中算家对微积分的早期认识和理解》，《自然科学史研究》2009年第1 期，第24-37 页。

[51]薄树人：《清代对开普勒方程的研究》，《中国天文学史文集》第3 集，北京：科学出版社1984年版。

[52]冯立昇、牛亚华：《李善兰对椭圆及其应用问题的研究》，李迪主编：《数学史研究文集》第三辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1992年版，第100-111 页。

[53]（清）李善兰：《级数回求》，《则古昔斋算学》金陵刊本，同治六年（1867年）。

[54]薄树人：《清代对开普勒方程的研究》，《中国天文学史文集》第3 集，北京：科学出版社1984年版。

[55]（美）罗密士，（英）伟烈亚力译，（清）李善兰述：《代微积拾级·李善兰序》，墨海书馆刊本，咸丰己未（1859年）。

[56]高红成：《李善兰对微积分的理解与运用》，《中国科技史杂志》2009年第2 期，第222-230 页。

[57]杜亚泉主编：《亚泉杂志》第3 册，微积学问答。

[58]李叔同主编的《乐石社社友小传》称：“王世，字匊昆，号菊悃。禹航西乡人，侨寓武林，喜探数理，兼有金石癖。”

[59]“谢译《微积学》”，指的是罗密士原著，潘慎文和谢洪赉合译的《最新微积学教科书》，商务印书馆1905年1月铅印出版。底本是Elias Loomis，Elements of Differential and Integral Calculus。参阅刘盛利、代钦：《清末罗密士的〈最新微积学教科书〉》，《数学教育学报》2012年第2 期，第11-13 页。

[60]王世：《微积学答问》，石印本，光绪三十三年（1907年）。

[61]王世：《代形合参解法·叙言》，石印本，光绪丁未（1907年）。

[62]冯桂芬、陈暘《西算新法直解》（8 卷，1865年），蒋士栋《微积释马》（1897年），张秉枢《代微积拾级补草》（1897年自序），林传甲《微积集证》（4 卷，1900年），杜亚泉《微积问答》（1 卷，1900年），佚名《微积互求表》（1 卷，1900年，载《两湖书院课程》中），徐异《积分难题》（1 卷，1901年），卢靖《叠微分补草》（稿本，1902年序），陈志坚《微积阐详》（5 卷，1905年），黄启明《微积通诠》（16 卷，1905年），周藩《代微积拾级详草》（1 册，1905年），王达鲁《微积新理》（1906年），王世《微积学问答》（1907年）。这些著作绝大部分集中在20世纪初出版（李兆华主编：《中国近代数学教育史稿》，济南：山东教育出版社2005年版，第207 页），这也表明国人对微积分的理解经历了一个过程。

[63]李兆华：《晚清算学课艺考察》，《自然科学史研究》2006年第4 期，第322-342 页。

[64]《毕乃德记福建船政学堂的分科及其课程》，见朱有瓛主编：《中国近代学制史料》第一辑上册，上海：华东师范大学出版社1983年版，第464 页。

[65]朱有瓛、高时良主编：《中国近代学制史料》第四辑，上海：华东师范大学出版社1993年版，第458-459 页。

[66]《（同文馆）光绪二年公布的八年课程表》，见朱有瓛主编：《中国近代学制史料》第一辑上册，上海：华东师范大学出版社1983年版，第71-72 页。

[67]《（同文馆）光绪四年各科岁试题》，同上，第89 页。

[68]（美）丁韪良：《格物测算·序》，同文馆铅印本，光绪九年（1883年）。

[69]郭金海：《京师同文馆数学教学探析》，《自然科学史研究》2003年增刊，第47-60 页。

[70]（美）林乐知：《中西书院课程规条》，朱有瓛、高时良主编：《中国近代学制史料》第四辑，上海：华东师范大学出版社1993年版，第286-287 页。

[71]《湘乡东山精舍章程》，见朱有瓛主编：《中国近代学制史料》第一辑上册，上海：华东师范大学出版社1983年版，第322-324 页。

[72]《绍郡中西学堂规约》，见朱有瓛主编：《中国近代学制史料》第一辑下册，上海：华东师范大学出版社1986年版，第736、742-744 页。

[73]《山东巡抚袁世凯奏办山东大学堂折（附章程）》，同上，第808 页。

[74]《苏云峰记两湖书院》，同上，第411 页。

[75]《微积互求表》，载《两湖书院课程·附表》，光绪二十四年（1898年）两湖书院刊本。此表应是后来刊刻与《两湖书院课程》合订。

[76]刘光蕡：《谕味经诸生》，同上，第381 页。

[77]《代微积拾级补草》是单行本，并没有收入《味经时务斋课稿丛钞·算术》[5种，《借根演元》《迳求和较》《盈朒公式》《勾股公式》《借根勾股细草》，光绪丁酉（1897年）八月味经刊书处本] 中，但版式与它们相同，单鱼尾，花口版心，上象鼻题“课稿丛钞”，版心题“代微积拾级补草”，有刘光蕡光绪丁酉夏的序。

[78]（清）张秉枢：《代微积拾级补草·跋》，味经刊书处刊本（单行本），光绪丁酉（1897年）。

[79]杨冰（1871—1913年），江苏东台人，数学家和数学教育家，曾被派遣到日本考察学制，并受日本数学家长泽龟田之助邀请讲学。他与崔朝庆合编了中国第一部近代学堂所用的综合科学用表《算表合璧》（1902年）。见陈克胜、郭世荣：《中国第一部近代学堂所用的综合科学用表——〈算表合璧〉》，《中国科技史杂志》2012年第1 期，第11-21页。

[80]《南菁书院部分课作题》，见朱有瓛主编：《中国近代学制史料》第一辑下册，上海：华东师范大学出版社1986年版，第423 页。

[81]梁启超：《湖南时务学堂学约（附读书分月课程表）》，朱有瓛主编：《中国近代学制史料》第一辑下册，上海：华东师范大学出版社1986年版，第306 页。

[82]（清）林传甲：《微积集证》，序，卷三跋，长沙督学使署刊本，光绪二十六年（1900年）。

[83]（清）黄启明：《微积通诠》，陈平瑛序，广州刊本，光绪三十一年（1905年）。

[84]（清）陈志坚：《微积阐详》，松江嵇文墨斋刊本，光绪三十二年（1906年）。

[85]高红成：《试论晚清学校的微积分教学：1859—1905》，《内蒙古师范大学学报》（自然科学汉文版）2013年第4 期，第471-477 页。

[86]樊静、冯立昇：《晚清天文学译著〈谈天〉版本考》，《内蒙古师范大学学报》（自然科学汉文版）2007年第6 期，第695-700 页。

[87]孙祝耆民国期间著有《成功之代数（上编）》（国高参考适用）一书，此书有“奉天省视学官”李国凤作的序。该序称孙氏“光宣间，主讲奉天两级师范学校数理选科以及师范本科，继续至十余年之久”。李国凤自称为孙氏“受业”，并称“今日国内中小学校教师，多出其门，国凤粗解算理，也是先生启发的”。此书由东方书店于“康德十年八月三十日”在沈阳发行。按，1934年，中国历史上的末代皇帝溥仪在日本政府的扶持下建立了满洲帝国，即所谓的伪满，改年号为康德，同年称为康德元年，溥仪称康德皇帝。康德十年即为公元1943年。

[88]陈平瑛曾在自著的《直乘法》的序中称：“中华民国二年（1913年）十一月闽侯陈平瑛仲容自序于广州，时年三十有五。”又，卢朋著光绪壬寅（1902年）四月给《中西算学题镜》作序称：“仲容丁酉举于乡，已以天算作惊人一鸣。今年才二十四，大集彬彬，又成不朽盛业。”由这两条可以推证陈氏生于1879年。

[89]陈平瑛：《中西算学题镜·卢朋著序》，广州西湖街珍藏阁，辛丑（1901年）刻本。

[90]黄启明：《微积通诠·陈平瑛序》，菁华阁，刊刻时间不详，有陈平瑛和张成桂1905年的两序。

[91]黄启明：《微积通诠》，卷十四，菁华阁刊本，出版社时间不详，有陈平瑛1905年序。中科院自然科学史研究所图书馆有藏。

[92]高红成、王瑞：《椭圆积分在中国的一个历史注记》，《数学的实践与认识》2012年第17 期，第251-257 页。