1.学生孙祝耆的课艺

《龙城书院课艺（算学）》己亥年（1899）第一题：

《谈天》云，凡有彗星现大率三次，测其赤道经纬度以推其椭圆道或抛物道之大小及方向，即可定其诸根数，而依法推其全道。原书但举是说，而未能详其法，能否演为算例或代数公式以明之。

《谈天》是伟烈亚力和李善兰合译的英国著名天文学家侯矢勒（John herschel，1792—1871年）The Outline of Astronomy 一书，1859年在墨海书馆出版，是中国翻译出版的第一部全面系统介绍近代天文学的著作。该书力主日心地动说和椭圆学说，并以牛顿的万有引力定律、开普勒三大定律予以论证。为地动、椭圆学说在中国的真正确立，以及天文学名词的翻译和牛顿力学定律及其相关名词术语在中国的初次引入等方面，均作出重要贡献。^[86]其中卷十一“彗星”介绍了彗星的形成和运行规律，称“若不知摄力之理，则慧之行无法能解之，奈端（即牛顿）已考绕日诸体，皆以圆锥诸曲线而行。因悟彗星道必依此理”。显然，要理解《谈天》中的知识必须具备必要的数学基础，特别是圆锥曲线方面的知识。

龙城书院教学显然涉及《谈天》，此题归入天文测算题，实即圆锥曲线轨道运动问题。该题录用了孙祝耆的课艺，在书中占26 页半的篇幅，可以说是一篇数学专题论文。孙氏对数学应该很有研究，在该题“推彗星距卑之椭圆面积第十二”的“本法”下有小字注释：“此法之理详见拙撰《恒斋算学》第一种。”惜《恒斋算学》未能得见，也不见诸算学书目。^[87]孙氏的解法简介如下。

如图3-5-1，设椭圆ACB 为彗星（P）的轨道，椭圆扇形AOP 的面积S椭圆扇形AOP 记为S，顶点A 为最卑点，向径F1P （记为r）扫过的面积SF1AP。从数学角度而言，就是要求出实行角∠AF1P （记为θ）与S 之间的关系式。算草主要步骤如下：

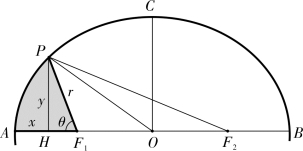
图3-5-1

以A 为原点、轴AB 为横轴建立坐标系，P 点坐标为（x，y），椭圆方程为，则

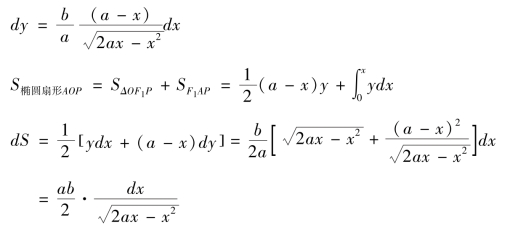
由《微积溯源》第126 款积分公式

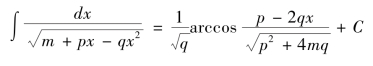
可得

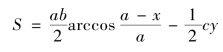
又

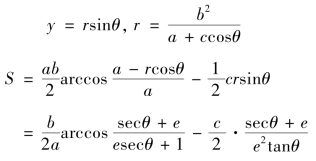
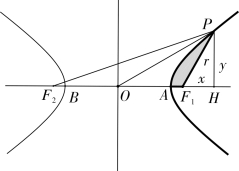
图3-5-2

当轨道为双曲线时，情况类似，如图3-5-2有

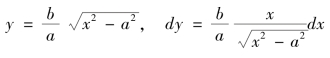
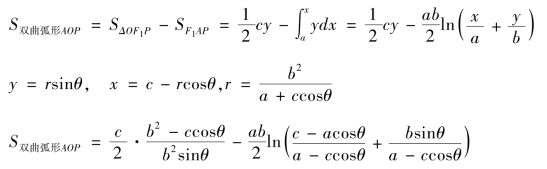
如前两章所述，圆锥曲线轨道运动问题，是清代自《历象考成后编》（1742年）刊刻以来天算家就一直关注的问题。孙祝耆的课艺实际上是用微积分方法解答了这一问题，较之他的前辈，方法已属于现代了。

2.龙城书院毕业生沈保枢对夏鸾翔两术的改进（1901年）

沈保枢，生卒年不详，阳湖人，是龙城书院的毕业生，《龙城书院课艺（算学）》收有他的多个课艺。沈氏对容圆问题和曲线求积问题颇有研究，著有《容圆通义》四卷（1901年）和《曲线剩义》八卷（1901年）。其中，《曲线剩义》卷三“双曲线求弧背术”与卷四“立双曲线求皮积术补”是对夏鸾翔《致曲术》中相关两术的订误，从中可以体现沈氏对圆锥曲线求积问题的认识以及对微积分的运用，同时也可以看出夏术相应的不足。

沈保枢《曲线剩义》卷三“双曲线求弧背术”部分（沈氏家刻红印本）

夏氏《致曲术》中“双曲线求弧背术”即本章第三节式（3.3.11），是关于y 的级数展开式，该式只有在0≤y≤时收敛，沈氏认为这是该术的不足，因此对该术进行改进。他指出夏术不足是因为“立术之初，既以纵线（y）为主”导致的，若“先于立术之初以横线为主”，则可以得“通术”。解题步骤简述如下。(www.daowen.com)

由《代微积拾级》第七卷第一款建立双曲线的方程

由《代微积拾级》第十四卷第八款得到弧长微分式

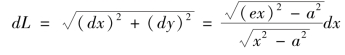
其中。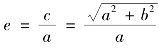

由《代数术》第一百六十款有

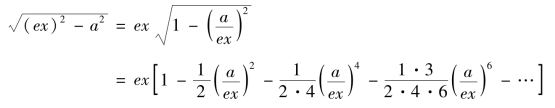
所以

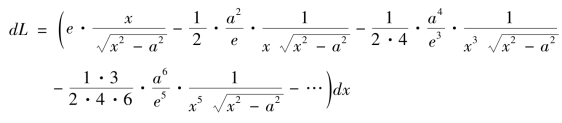
又由《代微积拾级》第十七卷第十三款第二术有

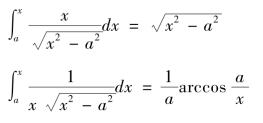
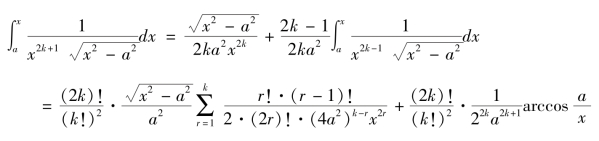
其中k=1，2，3…。

因此

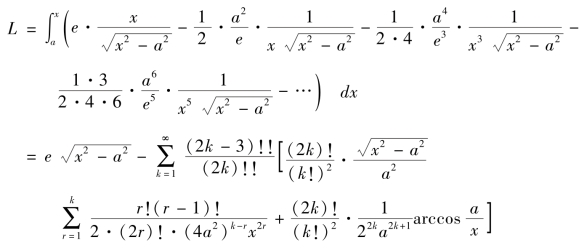
这里规定（-1）！！=1。

除最后的表达式为书写便利我们利用求和符号改写外，整个过程几乎照录。如果不考虑所用符号区别的话，沈氏的推算过程与现在无异。他的改进之处在于利用了式（3.3.1），使得展开式对于x≥a 均成立。沈氏最后说道：

细审此术，亦无他谬巧，惟立术之初以横线为主，则所化级数之式以求积分转折甚多，人每因此而中辍，枉费心血，莫此为甚。实则《溯源》《拾级》各式具备，融会贯通非难事也。

在《致曲术》中，夏氏对与双曲线绕实轴的旋转体（“笠体双曲线”“钟体双曲线”）表面积求法存目而无术，后来在《万象一原》中虽然得到一术，也存在着与“双曲线求弧背术”一样的不足，沈氏在《曲线剩义》卷四“立双曲线求皮积术补”中也是利用式（3.3.1）得到比较好的展开式。特别的，他指出就双曲线的方程而言，没有必要分“笠体”“钟体”，夏氏两术实则一术。在此简单介绍沈氏的推算如下。

通过双曲线方程并利用《代微积拾级》第十四卷第十款，得到双曲线绕实轴旋转体表面积微分式

又根据式（3.3.1）并积分得到

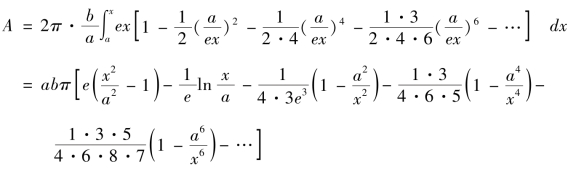
此式的优点是该展开式对于x≥a 均成立。

对照本章第三节夏氏的推算，明显的不同是，沈氏是采用双曲线的方程并按《代微积拾级》中微积分求面积的方法进行的。由于方法的改进，夏氏术的不足在沈氏眼中自然很明显。