张燨，生平不详，从他所著的《窃悟轩算草》（1898年）中的一些信息可以知道，他是云间（今松江）人，曾在融斋书院和南菁书院中学习，当时的数学教习为著名数学家刘彝程。1897年，张燨主讲濯秀书斋算学馆，给同乡友人或其子弟讲授算学。张氏有数学著作《窃悟轩算草》（1898年）和《堆垛术》（1903年），1906年他还曾给陈志坚的《微积阐详》作序。

《窃悟轩算草》收录了张氏在融斋书院和南菁书院“考试书院之作”，以及在濯秀书斋算学馆时考课学生课艺的“拟作”，共16 题20 草。这16 题中有3 题涉及微积分，其中也是“算草”的第一题为：

哈司韦椭圆求周恒失之大。今损其术，以长短径幂相加为和，相减为较，和较除之，又自之，为递次乘法。乘法乘单一，十六除之，为第一数；乘法乘第一数，三、五累乘之，四除之，十六除之，为第二数；乘法乘第二数，七、九累乘之，九除之，十六除之，为第三数。如是求得若干数，并之，以减单一。乃依哈术并长短径幂半之开方称周率三一四五九二六五得数以乘之为椭圆周。试证其法。己丑（1889年）拟作。

这里的“哈司韦”指的是江衡与傅兰雅合译的《算式集要》（4 卷，1877年）的原作者Charles Haynes Haswell （1809—1907年），“椭圆求周”指的是《算式集要》卷三给出的椭圆周长公式p=。张氏认为此公式不精确，偏大。他运用微积分方法得到了椭圆周长的级数公式，具体运算过程中运用了三角代换，与《代微积拾级》和《微积溯源》中的椭周求法并不相同。他的主要步骤用现代数学符号表达如下：

其中。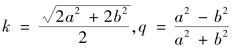

然后张氏找出cos2θ 各次幂的降次展开式，借用组合符号表示如下：(www.daowen.com)

其中m=1，2，3，…。

张氏指出在θ→积分过程中，cos2θ 的奇次幂的结果为0，偶次幂仅需考虑展开式中的常数项，最后他得到椭圆周长公式为

比较可知，《算式集要》中的椭圆周长公式偏大。

这个算草虽是张氏为自己的学生所作的范例，但肯定与他早年的学习有关，他的运算方法和符号用法与传入的两部微积分译著一致，可谓运用自如。