椭圆轨道运动问题实质是椭圆部分面积的计算，涉及微积分方法的运用，椭圆的向径r 与实引角α 之间的关系[式（4.2.1），第四章将介绍] 是这个问题的基本关系式。依据《代微积拾级》，这个问题完全可以直接按照微积分的方法得到椭圆向径扫过面积

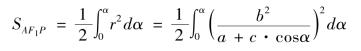
可是从上文的分析可以看出，虽然李善兰在解答过程中提到“微分”与“积分”，但他的基本方法是先得到某个量y 的微分关于另外一个量x 的级数解析式dy=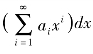，这个级数依据割圆连比例法得到。然后逐项积分得到y 关于x 的幂级数表达式y=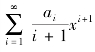，最后运用垛积术与级数回求法得到x 关于y 的幂级数表达式，所得成果结构如图3-4-4。这些成果反映了李氏对《代微积拾级》传入的微积分的认识和理解。

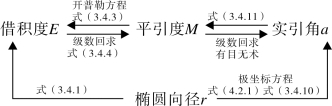
图3-4-4

我们再看看李善兰自己对微积分的解读，他在给《代微积拾级》作序时说：

其理之大要，凡线面体皆设为由小渐大一刹那中所增之积，即微分也，其全积即积分也。故积分逐层分之为无数微分，合无数微分仍为积分。其法之大要，恒设纵横二线，以天代横线，以地代纵线。以代横线之微分，以代纵线之微分。凡代数式皆以法求其微系数，系于或之左，为一切线面体之微分。故一切线面体之微分与纵线之微分皆有比例，而叠求微系数可得线面体之级数、曲线之诸异点。是谓微分术。^[55]

在此，李善兰眼中的微分术就是“叠求微系数”，即函数的级数展开式的求法，这与上一节夏氏的认识几乎一致。

可见，李善兰眼中的微分术就是求函数的级数展开式和曲线的“诸异点”（如驻点、拐点等）的求法，主要是“叠求微系数”，即幂级数展开式。所以《椭圆拾遗》第33 款称：距心线之级数为借积度求平引面积之微分。类似的表述还有第39 款（距心线级数自乘大小二半径各除依次得实引度求平引度之微分）和第42 款（距心线级数自乘大小二半径各除依次为实引度求平引度之微分）。(www.daowen.com)

在《代微积拾级》中运用泰勒公式和麦克劳林公式求幂级数展开式，通过前文的分析发现，李氏并没有理会这两个公式，他得到幂级数展开式是运用连比例四率法（如图3-4-2）与中国传统数学中的垛积术以及级数回求术。如本章第一节所述，这种方法是董祐诚在《割圆连比例术图解》中为探求“杜氏三术”立术之源而发展起来的。李氏对此颇有研究，他在其《垛积比类》题解就称：“垛积为少广一支，……西人代数微分中所有级数大半皆是，其用亦广矣。”

可见，李氏将微分术等同于幂级数展开式的求法，而幂级数展开式的求法则是秉承清代中期逐渐发展起来的幂级数展开法，并不求助于泰勒公式和马克劳林公式。李善兰这种将微分术等同于幂级数展开式的求法的做法，在微积分传入中国初期具有代表性。第三节中夏鸾翔的《致曲术》及《万象一原》在解决二次曲线求积问题时也是这样处理的，只不过他得到幂级数展开式的方法是运用他更为熟悉的递加数。这种做法是有局限性的，伟烈亚力曾批评说：“因不用代数式，故或言之甚繁，推之甚难”，而且也提到了“李君秋纫所著各书”，与伟烈亚力在墨海书馆共事七八年的李善兰何以漠视了这个中肯的批评呢？

应注意的是，在《椭圆拾遗》中，李氏倒是吸收了《代微积拾级》中级数展开式的符号代数表示法，如式（3.4.10）表示为

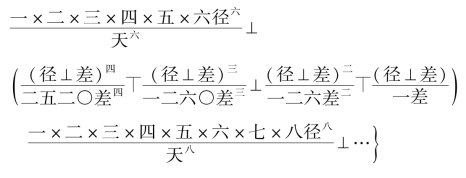
其中，即为α。这种表示使得运算和说理要简洁得多。自然要比夏鸾翔的递加数表示法简捷，也更有利于传播。从中可以看出李善兰对《代微积拾级》中符号代数的吸收。但李氏也就到此为止，他并没有对《代微积拾级》中诸如解析几何、泰勒公式、麦克劳林公式等更为深刻的数学知识进行深究。之所以第44 款由式（3.4.11）用级数回求法求实引角α 关于平引度M 的级数展开式时仅有目而无术，是因为运用级数回求法即使用代数表示法也很难归纳出级数系数的规律。

总之，李善兰对椭圆轨道运用问题的研究较之前人更为深刻，抓住该问题的本质关系，运用微积分思想和级数的方法得到一系列的创新成果。他将微分术等同于幂级数展开式的求法，而幂级数展开式的求法则秉承董祐诚割圆连比例术和级数回求法，并不求助于《代微积拾级》中的泰勒公式和麦克劳林公式。这表明微积分传入中国初期中算家对其的认识、理解和吸收程度，与他们自身知识结构有关。^[56]