在《椭圆拾遗》卷一第16 款中，李善兰用几何方法得到椭圆向径（r）与实引角（α）的关系式（第四章第二节将介绍），卷三的第36—38 款，第41—42 款在第16 款的基础上给出了r 关于α 的级数展开式。

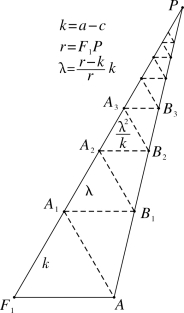
图3-4-2

如图3-4-2，椭圆向径r=F1P，卑径F1A 记为k=a-c，在F1P 上依次取点A1，A2，A3，…，使得F1A1=F1A=k，A1B1 ∥F1A，B1A2 ∥A1A，A2B2 ∥F1A，B2A3 ∥A2B1，A3B3 ∥F1A，…不难证明

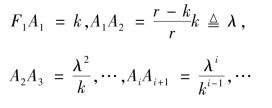
由此得到向径的一个关于的级数展开式

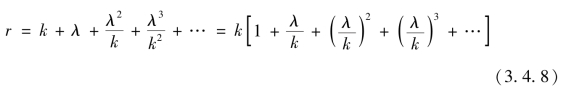
又由卷一第16 款r=[第四章第二节式（4.2.1）] 知道

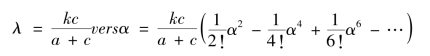
所以

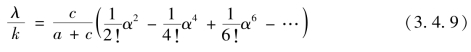
将式（3.4.9）代入式（3.4.8），合并同类项，得到r 关于α 的级数展开式(www.daowen.com)

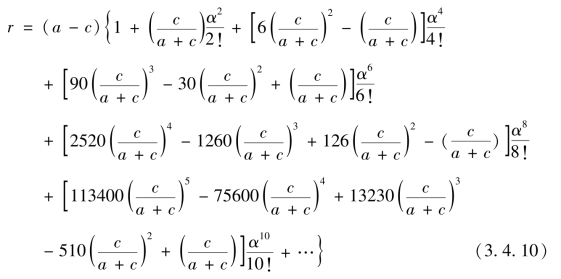
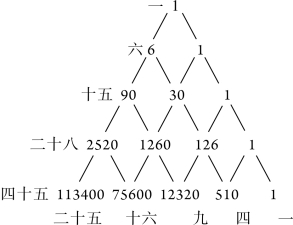
图3-4-3　系数递增之图

可以看出，式（3.4.10）中项的系数式是关于的多项式，不考虑符号，其系数的变化规律李善兰给出了“诸系数递增之理”。如图3-4-3，

第一层为天二之系数，第二层为天四之系数，三、四、五层为天六、天八、天一〇之系数。其递增之法向左斜行而下，第一次六倍，第二次十五倍，第三次二十八倍，第四次四十五倍，……顺是以下可类推。向右斜行而下第一行递一倍，第二行递四倍，第三行递九倍，第四行递二十五倍，……顺是以下可类推。设欲求某数，必先有本数上层之左右二数，左数向右斜行，右数向左斜行，各依法倍之，并二倍数即本数。

用Anm 表示第m 层从右向左第n 个数，则依照推算有

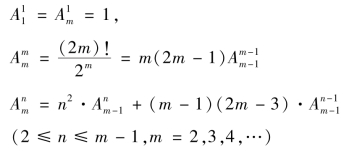
从推导过程可以看出，式（3.4.10）实际上是椭圆极坐标方程

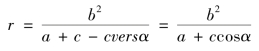
对实引角α 的幂级数展开式。