《椭圆拾遗》第33 款：“距心线之级数为借积度求平引面积之微分”。如图3-4-1，⊙O（OA）是椭圆大辅圆，⊙O（OF1）是以c 为半径的圆，∠AOQ 为借积度E，SAF1Q 为平引面积。该款结论为：F1Q 所对应的椭圆向径F1P （记为r）是平引面积的微分dS。

如图，QR 为大圆的切线，过F1 作F1H ⊥OQ 交OQ 于H 点，QR ∥F1H，若底QR“渐小变为点，则切线、弧线合二为一”，则平引面积为ΔQRF1 由“无数细三角所积而成”。借用现代数学符号表示，即当QR→0 时，SAF1Q=∫SΔQRF1，或SΔQRF1=dSAF1Q

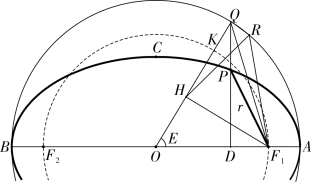
图3-4-1

又ΔQRH，ΔQRF1 为同底等高的两个等积三角形。所以

SΔQRH=dSAF1Q

因为QR→0 时，“切线、弧线合二为一”，则

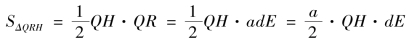
因为是常数，李氏把QH 看成是“平引面积微分”。

由图可知，AD=aversE，KH=cversE，所以。又根据卷一第14 款结论（见第四章第二节）有

所以

KH=r-(a-c)

又如图可知

KH=QH-QK=QH-AF1=QH-(a-c)

所以

QH=F1P=r

所以距心线r 为平引面积微分，即

如图3-4-1知，QH=a-c+c·versE，所以r=a-c+c·versE，中算家早就知道展开式

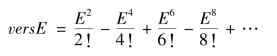
便得到向径（r）关于借积度（E）的级数表达式

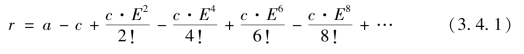
所以

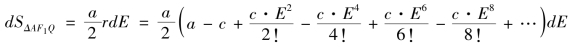
此即第33 款“距心线之级数为借积度求平引面积之微分”的现代数学表示。

由第33 款结论，可得平引面积的级数表达式

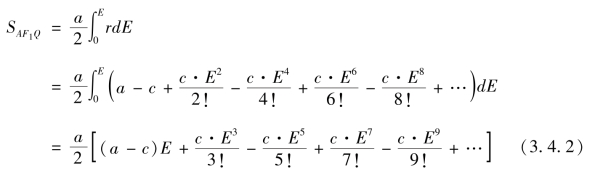
这便是第34 款“有距心线级数求平引面积”的结论。

又因为，M 为平引度（见第二章第一节），便得到平引度（M）关于借积度（E）的级数展开式

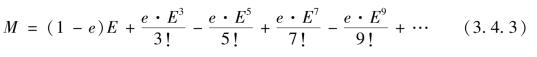
其中e=。显然，这是开普勒方程M=E-esinE 中M 关于E 的级数展开式。

第35 款：“有借积度求平引度之级数，即可得平引度求借积度之级数”。即由式（3.4.3）得到E 关于M 的级数展开式

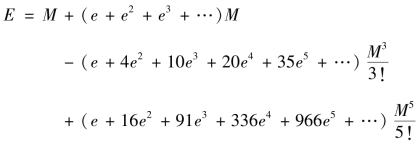
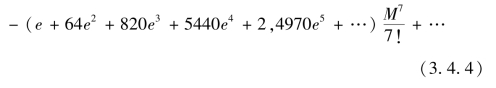
式（3.4.4）相对于李善兰原术形式作了改写，其中e=。此即开普勒方程关于E 对M 的级数解析式。

李善兰得到式（3.4.4）的方法为级数回求术，下面依据李氏的《级数回求》简单介绍其推导过程。

式（3.4.3）两边平方有

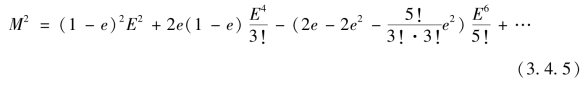
式（3.4.3）×式（3.4.5）有

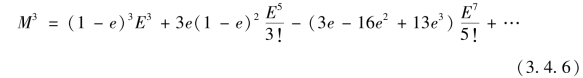(www.daowen.com)

式（3.4.5）×式（3.4.6）有

……

式（3.4.3）+e×式（3.4.3）+e2×式（3.4.3）+e3×式（3.4.3）+…有

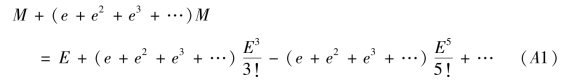
式（A1）-×（3.4.3）有

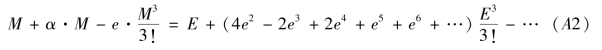
其中α=e+e2+e3+…

式（A2）-×（3.4.3）有

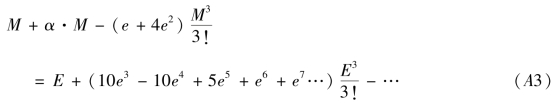
式（A3）-×（3.4.3）有

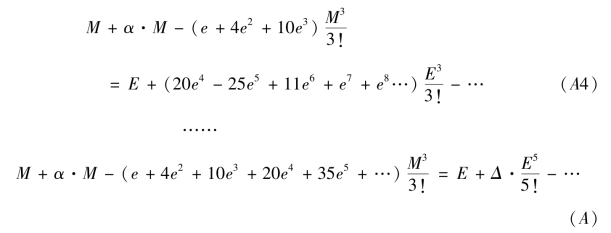
注意式（A）右边缺项，项的系数式待定，用Δ 表示，下同。至此，可以看出式（A）左边项的系数式是一个关于e 的级数展开式，不妨设为β，即

β=e+4e2+10e3+20e4+35e5+…

李善兰发现β 级数的系数列是三角垛的三乘垛各项之数。

注意到式（A2）右边项的系数式为-（e+11e2-19e3+11e4+e5+e6…），式（A3）中项的系数式为-（e+11e2+21e3-69e4+41e5+e6+e7…），……，依照项的消法，消去项得到

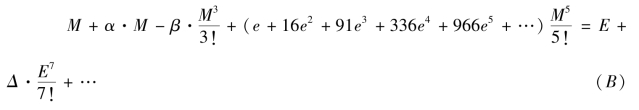
令式（B）中项的系数式为γ，李氏发现γ 级数的系数列依次是五乘垛第j 个数与六乘垛第（j-1）个数的10 倍之和，j=1，2，3，…。

依此方法李氏得到式（3.4.4），其中项的系数式级数的各项系数依次是七乘垛第j 个数、八乘垛第（j-1）个数的56 倍以及九乘垛第（j-2）个数的280 倍相之和，j=1，2，3，…。所以式（3.4.4）可表示为

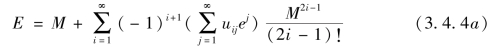
其中

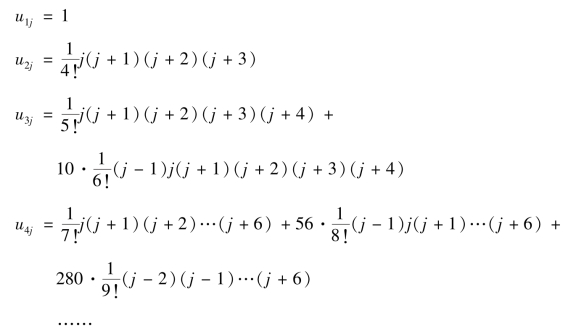
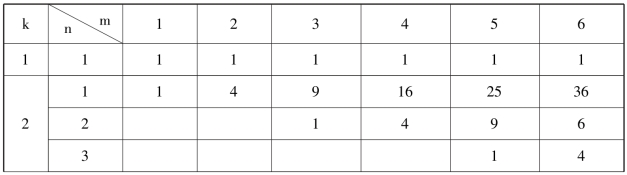
为了更为简洁表达项的系数式级数的系数列{uij}，李氏设计了一个数表，称之为“蝉联数表”（如表3-4-1）。

表3-4-1　蝉联数表

（续表）

用Lkmn 表示蝉联数表中第k 层第m 列第n 行之数，空白格可视为0，如L361=1296。

造表法为：

第一步，确定各层第1 行各数。第1 层第1 行之数均为1，且只有1 行。

=m2(k-1)，k=1，2，3，…，m=1，2，3，…

第二步，确定第2 层各行之数。将该层第1 行各数后错2 列放入第2 行，第2 行各数再后错2 列放入第3 行，即

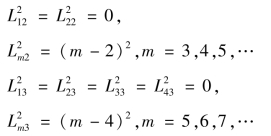
第三步，确定第k （k≥3）层的各列的第2 个数，它们基于第2 层各列的前2 个数具有递推性，

第四步，确定第k （k≥3）层的各列的第3 个数，它们基于第2 层各列的前3 个数具有递推性，

因此式（3.4.4a）中项的系数式级数的系数列{uij} 可以用蝉联数表中数表示

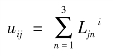
由第二章第一节知道，以积求角术中只是近似计算，原因是开普勒方程相对于借积度E 而言是超越方程，没有初等解。李善兰在《椭圆新术》中将利用式（3.4.4）求得E，然后求出实引角α。因此，李氏得到开普勒方程的无穷级数解法，在中算史上是首次。^[54]