1.项名达及其《椭圆求周术》

项名达继董祐诚之后对椭圆周长进行研究，并且是获得正确的椭周公式的第一人。项名达（1789—1850年），字步莱，号梅侣，浙江钱塘（今杭州）人。嘉庆二十一年（1816年）举人，考授国子监学正。道光六年（1826年）进士，改官知县，不就职。在此前后，在京居住多年，专心治学。在此期间，项氏结识了陈杰、黎应南和朱鸿。其中，陈氏当时为国子监算学助教，曾在钦天监任职，徐有壬曾从他学算。黎氏为李锐的弟子。项氏大约在道光十二年（1832年）离开北京，返回故里，担任余杭苕南书院主讲。十七年（1837年）回到杭州，在紫阳书院执教。二十六年（1846年）冬，因年岁高辞职回家。他的著作有《下学庵算术三种》[《勾股六术》一卷（1825年）]、《三角和较术》一卷（1843年）、《开诸乘方捷术》一卷（约1845年），有未完稿《象数一原》六卷（1843年自序），还有一部《割圆捷术》一卷，但未见传本。

项名达对椭圆周长的研究体现在《象数一原》卷六中的《椭圆求周术》。陕西富商杨尚文资助出版的《连筠簃丛书》中收入项名达《椭圆术》一卷，该卷与《椭圆求周术》文字基本相同，但较其他版本多了跋文，该跋文中有明确的时间和地点信息，他称：

……总论曰以四术求椭圆周为本术。……然则圆理无穷。一递加数，有以括之矣。诚妙矣哉。道光辛卯（1831年）梅侣项名达校定于都城槐荫馆。^[21]

又，黎应南道光壬辰（1832年）为项名达的《勾股六术》作序，曾称：

梅侣尝立有弧三角总较术，求椭圆弧线术，术虽定，未有诠释，余促成之，而义奥趣幽，非旦夕可竟事。

又，项氏临终前在《象数一原》自序（1849年）中称：

向玩弦矢诸率，会得递加数，复析圜，得两等边三角，其象适与数会，因草成《图解》一册，聊自达意，而疎脱甚多。……杨缃芸农部在京见旧刻《割圜捷术》序中言及《图解》，亟思一见。丁未（1847年）冬来杭见访，因示以所编。缃芸谓，书未半而君年垂迈，是书断不可不成，且不可缓成，克期以一载。临别尚谆切致嘱，余感其意为之，定书名曰《象数一原》。

其中，杨缃芸，福建侯官人，名宝臣，笃嗜算学。^[22] 《连筠簃丛书》中收有罗士琳的《勾股截积算术》二卷，就是由杨宝臣校算。

由以上三条可知，项名达至迟在1831年，就已经得到椭圆周长公式。他撰写《象数一原》始于1837年，直至1850年逝世还未完稿。在书中，项氏想给椭圆求周术一些详细解释，但已到垂暮之年，加之病势沉重，力不从心，他只好把几个结论性的成果记下来，列于《象数一原》卷六之末，这也就是椭圆求周术和几个关键步骤：决定加减差之备数法、求与平弧相应之逐分椭圆通弦、求逐分椭圆抵周线。并向后人表示“向思纂明之，而病躯不能从事。姑发其意，以俟知者”。1848年冬，项名达又致函他的好友戴煦称，“弦矢互求”“椭圆求周”为自己惬意之作，但“病体颇顿，精力日衰，弦矢术或勉力成之，椭圆则不能著解矣”，希望戴煦代为整理成篇。1850年项氏辞世。1857年，戴煦为《椭圆求周术》加上按语，并作《椭圆求周术图解》，补成《象数一原》卷七。

2.项名达椭圆求周术

现今对项名达椭圆求周术的研究比较多，也较为成熟。李俨先生较早对项名达椭圆求周术数理过程进行讨论。^[23]何绍庚的《椭圆求周术释义》在李俨先生研究的基础上，对项氏椭圆周长推理过程进行了详细的解读，并探讨项氏方法的基础和来源，很有启发意义。^[24]牛亚华的《项名达的椭圆求周术研究》在指出何文推理过程的一个错误的基础上，对项氏椭圆求周术的推导过程进行重新的梳理。^[25]本节在何文研究的基础上，参考其他两家的研究以及原文，对项氏的推导过程进行简要说明。

项名达在《椭圆求周术》总论中说：

以上四术，求椭圆周为本术，后三术为求椭圆所由来，故备载之。有抵周线术，而各椭弦可求。有椭弦术，而各椭弦和可求。椭弦和既可求，椭圆周即无不可求。其用全在逐分倍外矢。各三率不齐，须以倍外矢齐之。倍外矢不齐，又须以半径齐之。所以能齐其不齐者，则恃有递加数一图与之婉转而符会。观后图解便可洞然。夫求平圆线非递加数，而其率不通。今求椭圆弧线亦复如是。然则圆理无穷，一递加数有以括之矣。诚妙矣哉。

这段话概括地给出了椭圆周长公式的推导步骤，具体说来是相当繁琐和复杂的，现根据他的简短说明和戴煦的图解，大体说明如下。

如图3-2-2，为象限椭圆周，为其对应的象限大辅圆，将等分，Q0（A），Q1，Q2，…Qi，Qi+1，…，Qn-1，Qn（B′）为分点，一分大圆弧对应的弦长为QiQi+1。过点Qi（i=1，2，…，n-1）作长轴的垂线交椭圆于点Pi，垂足为Ki（i=1，2，…，n-1），则相应得到与QiQi+1 对应的一分椭圆弦长PiPi+1。过点Pi，Qi 分别作Pi+1Qi+1 的垂线，垂足分别为点Mi+1，Ri+1，在Ri+1Qi+1 上取点Ni+1 使得Ri+1Ni+1=Mi+1Pi+1。为书写简便，记QiQi+1 为Ci，PiPi+1 为ci，Ri+1Qi+1为Ai，Ri+1Ni+1 为ai，QiRi+1 为Bi，∠Ri+1QiQi+1 为θi。

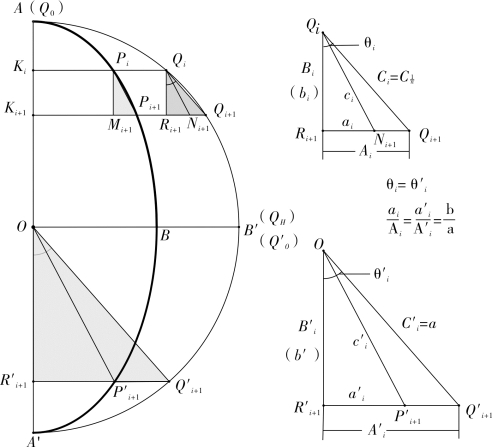
图3-2-2

由椭圆基本定理：

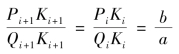
又由比例性质有

即

Ci 为n 分之一象限大圆弧的弦长，等于，ci 为Ci 对应的椭圆通弦（椭弦）长，RtΔQiRi+1Qi+1，RtΔQiRi+1Ni+1 为一组同股（Bi=bi）勾股形，有，所以

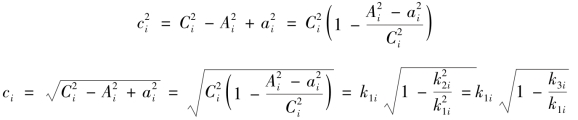
由第一节提到的二项式平方根展开式（3.1.6）可以得到

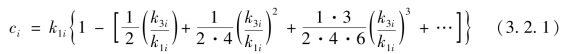
其中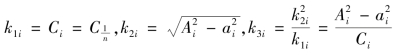，i=0，1，2，…，n-1，而k3i 被戴煦称为“椭圆通弦（ci）之三率”。

又如图3-2-2，从B′起在大辅圆弧取点Q′0（B′），Q′1，Q′2，…Q′i，Q′i+1，使得，i=1，2，…，n，过点Q′i+1 分别作长轴的垂线交椭圆于点 P′i+1，垂足为 R′i+1（i=1，2，…，n-1）。RtΔOR′i+1Q′i+1，RtΔOR′i+1P′i+1 为一组同股勾股形，其中OP′i+1 为椭圆抵周线，即椭圆半径。为书写简便，记OQ′i+1 为C′i，OP′i+1 为c′i，R′i+1Q′i+1 为A′i，R′i+1P′i+1 为a′i，OR′i+1 为B′i，∠R′i+1OQ′i+1 为θ′i。

因为

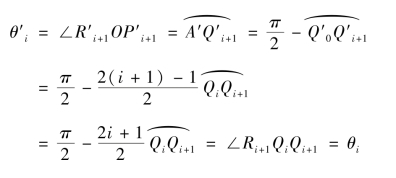
所以能得到

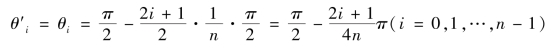(www.daowen.com)

同时可得

故

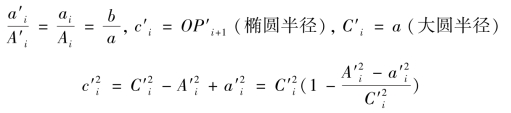
记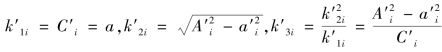，i=0，1，2，…，n-1，其中k′3i 被称为“抵周线（c′i）之连比例三率”。容易知道，

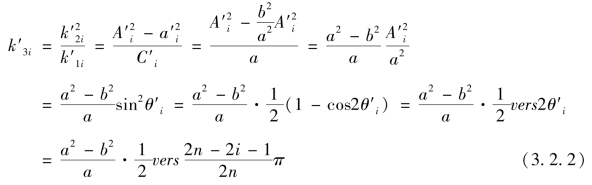
由椭弦三率与抵周线三率之间关系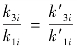，，结合式（3.1.2）得到

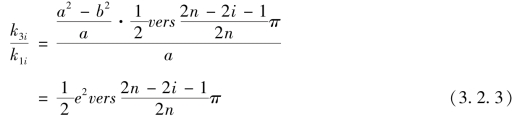
将式（3.2.3）代入式（3.2.1），得到

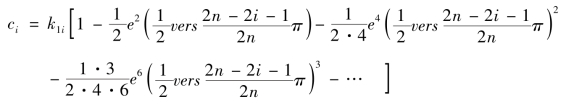
故

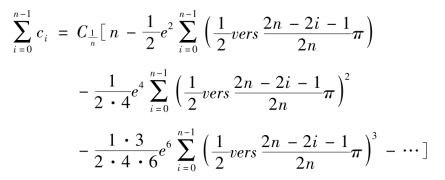
项名达将象限大辅圆一等分、二等分、三等分、四等分、五等分、六等分，分别计算出相应正矢各次幂级数之和，寻找规律，通过类比归纳得到，当p≤2n-1 时，

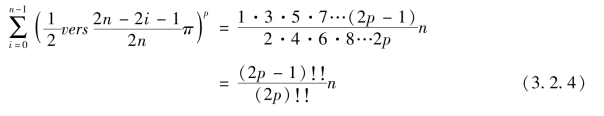
故

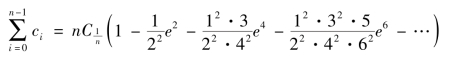
为象限椭周的椭弦和。

项名达最后指出：

一象限析分愈多，则椭弦渐与弧合，加减差愈后，而其差愈微，析至无量分，则椭弦和即椭圆象限，亦无加减差可言矣。

“析至无量分”时，即n→∞时，椭弦和趋近于椭圆周，同时辅圆通弦和趋近于辅圆周长，即

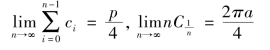
进而得到椭圆周长公式

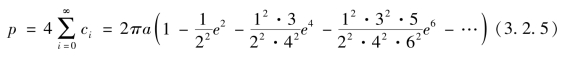
项名达《象数一原》（卷六）椭圆求周术（通汇本）

项名达推导椭圆求周公式的基本思想是用椭弦和逼近椭圆周，即用内接折线无限增多以逼近曲线的方法。这使他找到了解决椭圆周长问题的正确途径。在解决这一问题的过程中，他主要应用了椭圆基本定理、二项式平方根的级数展开式[上一节式（3.1.6）] 以及等分圆周时正矢各次幂的级数求和公式[式（3.2.4）]。椭圆基本定理早已有之，而后两项则是项名达独立研究的成果，也正是推导椭圆周长公式的关键。^[26]

项名达所使用的推导方法，实质上是继承和发展了中国古代传统的割圆术。这种方法已经包含了对直线和曲线相互转化关系的一定认识。

中国古代的割圆术虽然包含了直曲转化的辩证思想，但基本上局限于计算圆周率、圆面积和圆弧长度等问题。清初数学家明安图和稍后的董祐诚，将其发展成割圆连比例法，解决了一系列无穷级数问题，但是这些问题仍未脱离对圆及圆内线段的研究。项名达首先突破了割圆术原有的应用范围，通过椭圆基本定理，将割圆连比例法应用到椭圆上，拓展了二次曲线的研究领域，从而把对直曲关系的认识提高到一个新的水平，使古老的割圆术迸发出新的光彩。所用方法与现今椭圆积分原理相符，惟其方法初等因而运算量比较大。

直曲转化离不开极限，项名达在用内接折线逼近椭圆圆周时，明确指出“分极于无分，则差入于无差”。这就是说，当折线无限增多的时候，椭弦和与椭圆周之间的差就逐渐消失了，它的极限就是椭圆周长，亦即所谓“椭弦渐与弧合”。在用内接折线逼近圆周推导弦矢公式时，他指出：“假其有尽者，察数之变；而还其无尽者，得理之通。”这句话概括地表达了项名达通过有穷研究无穷和运用极限过程的基本思想。由于具有割圆术的基础、一系列辩证思想以及熟练的数学技巧，才使得他运用初等数学方法，却获得了包含高等数学内容的杰出成就。

戴煦在校补《象数一原》之后指出，项氏椭圆求周公式（3.2.5）是“借大积”开平方以大辅圆立算，因而也可以“借小积”开平方以小辅圆立算。所谓借小积开平方，即第一节提到的式（3.1.7）。由此戴煦得到另一个椭周公式

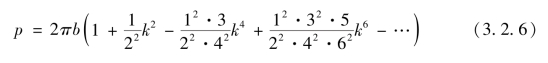
其中，k2=。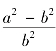

项、戴之后，徐有壬、夏鸾翔二人也对椭圆周长进行了研究。徐氏结果与项、戴二氏相同。夏鸾翔是项名达的入室弟子，对椭圆周长等二次曲线求积问题有独到的研究，所用方法较之项、戴二氏更为一般。他得到更为一般的椭圆弧长公式，椭圆周长成了其中一种特殊情形。详细讨论见下一节。