如前文所言，李善兰鉴于徐有壬的《椭圆正术》叙述比较简洁，有些步骤一般学者难以领悟，因此作《椭圆正术解》。从他所说“客窗多暇，辄逐术为补图详解之”的话来看，大约是他1852年去上海以后或者1860年在徐有壬的江苏巡抚衙门中作幕客时所作。可能在完成《椭圆正术解》之后，他又对两法提出新的见解，写成《椭圆新术》。李氏的“新术”只有两术，其一是改进“以角求积”术，其二就是给出了开普勒方程的幂级数算法。

1.对“以角求积”术的改进

李善兰的《椭圆新术》改进了“以角求积”术，如图2-3-3，各点、线的意义参见本章第一节，在这里李氏引入所谓的“平圆积角”，即∠AF1Q。第一步，由椭圆基本定理有，得到∠AF1Q，即“平圆面积角”。

图2-3-3

第二步，求较角∠OQF1，在ΔOQF1 中运用正弦定理有，得到∠OQF1，称之为“较角”。借积度为平圆积角与较角的差，即E=∠QOF1=∠AF1Q-∠OQF1。

第三步，求（E-M），李氏命之为“积差”。

由椭圆基本定理有

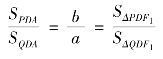
故

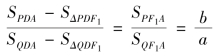
故

又

故

SQF1A=S扇形Q′OA

故

S扇形QOA-S扇形Q′OA=S扇形QOA-SQF1AS扇形Q′OQ=SΔQOF1

即

作F1K ⊥OQ，则有

故

又因为 ΔQDO ∽ΔF1KO

故

故

此式即开普勒方程

M=E-esinE

可以看出，李氏的方法相较以前的有很大的改进，使得“以角求积”术更简洁明了，过程也简化很多。=F1K 的证明，相当于将弧线转化为线段，使得扇形Q′OQ 面积转化为了三角形ΔQOF 面积。

2.开普勒方程的级数解答

根据M=E-esinE 有

aM=aE-csinE

令对应于角M 和角E 的大辅圆上的弧长为Ms，Es，即Ms=aM，Es=aE，李善兰给出级数展开式

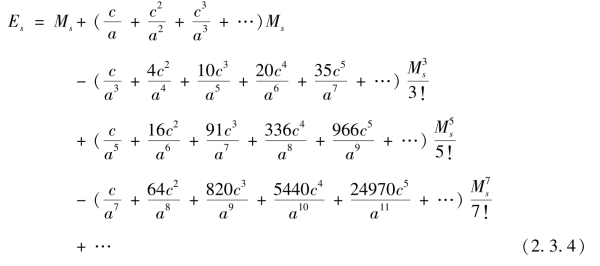
由此式可得到实引角α。

式（2.3.4）实质是用无穷级数解开普勒方程，这在中国数学史和天文学史上均是开创性的成果。^[50]其推导过程我们将在第三章第四节展开论述。

李善兰《椭圆新术》（续修四库全书本）

乾嘉学派的学者在治经的过程中并不是仅仅运用传统天文数学成果，欧洲天文学从一开始就是他们的重要工具。他们几乎都对欧洲历法及其相关的平面、球面三角学等都做过研究。被视为“中学”代表的李锐总是试图完备地、演进地、一般地解决所探讨的数学问题。焦循则发明了符号法，并且也如李锐一样坚持一般性的研究方法，他们的证明方法大多来自传统数学，他们对严谨性的追求肯定受到考据学及易学治学方法的影响，但也与传入的欧洲数学的方法和特点若合符节。^[51]中国数学研究从算法研究转化为纯粹的学术研究，一些数学家致力于对传入的数学知识的证明和深化研究甚至是理论层面的研究，徐、李二人的“正术”和“新术”显然不再是解释性的重复工作了，而是含有高超的数学技巧和思想，非专门研究不可得。

梁启超曾评价清代算学说：

清代算学，顺、康间仅消化西法，乾隆初仅杂释经典。其确能独立有所发明者，实自乾隆中叶后，而嘉、道、咸、同为盛。推厥所由，则皆天元、四元两术之复活有以牖之。徐文定（指徐光启）所谓“会通以求超胜”，盖实现于百年之后矣。^[52]

他将乾嘉以后治算之人分为三类^[53]：

第一类是奉职于钦天监的台官。他们因为工作的便利，占有资料较多，测天的仪器设备较为齐备，对于历算容易有新发明。如明安图的《割圆密率捷法》、博启的《勾股形内容三事和较》。

第二类是经师。他们并非算学名家，因为研究经学经典或研究历史需要天文历算方面的知识，而以历算作为副业。算学于他们而言只是解释、考据经典的工具。这一派发源于黄宗羲、惠天牧，到戴震、钱大昕达到顶峰，其后如焦循、阮元、顾栋高、程瑶田、凌廷堪、孔广森等人均如此。他们的目的大都在于借天文历算来解决经学或史学问题，对历算本身并没有太多的发明与创新。但后来的历算名家大都出于他们门下，如李锐师从钱大昕、罗士琳师从阮元。

第三类就是专门的算学家。“专门算家，自王（锡阐）、梅（文鼎）以后，中绝者垂百年，至嘉庆间始复活，道、咸间乃极盛。”初期主要人物是焦循、李锐和汪莱三人。他们的兴趣几乎都在研究和解决数学问题，对于经学或史学的一些问题倒没有什么创见。

本章三节所论述的对椭圆模型的数学问题的研讨，与梁氏对治算学者的分类刚好可以分别对应。

【注释】

[1]《圣祖实录》，卷二四六，北京：中华书局。

[2]韩琦：《“蒙养斋”的设立与〈历象考成〉的编纂》，陈美东：《中国科学技术史·天文学卷》，北京：科学出版社2003年版，第665-667 页。(www.daowen.com)

[3]韩琦：《清代前期中国天文学体系的逐渐转变》，杜昇云等主编：《中国古代天文学的转轨与近代天文学》，北京：中国科学技术出版社2008年版，第174 页。

[4]薄树人：《清代对开普勒方程的研究》，《中国天文学史文集》第3 集，北京：科学出版社1984年版。

[5]Shi，Yunli Reforming Astronomy and Compiling Imperial Science in the Post-Kangxi Era：The Social Dimension of the Yuzhi lixiang kaocheng houbian 御製曆象考成後編，EASTM 28（2008），pp.36-81.

[6]韩琦：《清代前期中国天文学体系的逐渐转变》，杜昇云等主编：《中国古代天文学的转轨与近代天文学》，北京：中国科学技术出版社2008年版，第185-186 页。

[7]《和硕庄亲王允禄等奏折》，见《御制历象考成后编·奏议》，光绪丙申（1896年）秋励志书屋刊本。

[8]郭世荣、李迪：《葡萄牙传教士徐懋德在钦天监的天文工作》，《山东科技大学学报》（社会科学版）2011年第2 期。

[9]本章参考的《御制历象考成后编》为光绪丙申（1896年）励志书屋刊本。

[10]李俨：《中算家的圆锥曲线说》，《李俨钱宝琮科学史全集》第七卷，沈阳：辽宁教育出版社1998年版，第491-514 页。

[11]薄树人：《清代对开普勒方程的研究》，《中国天文学史文集》第3 集，北京：科学出版社1984年版。

[12]牛亚华：《明末清初椭圆知识的传入及应用》，李迪主编：《数学史研究文集》第一辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1990年版，第104-116 页。

[13]梅文鼎：《平三角举要》，《中国科学技术典籍通汇·数学卷》第四册，郑州：河南教育出版社1993年版，第472、490 页。

[14]石云里：《〈历象考成后编〉中的中心差求法及其日月理论的总体精度——纪念薄树人先生逝世五周年》，《中国科技史料》2003年第2 期，第132-146 页。

[15]刘默：《乾嘉学术十论》，北京：三联书店2006年版，第272 页。

[16]钱大昕：《嘉定钱大昕全集》第一册，南京：江苏古籍出版社1997年版，第12页。

[17]钱大昕：《嘉定钱大昕全集》第一册，南京：江苏古籍出版社1997年版，第15页。

[18]江藩：《汉学师承记》，北京：三联书店1998年版，第52 页。

[19]钱大昕：《潜研堂文集·戴先生传》，《嘉定钱大昕全集》第九册，南京：江苏古籍出版社1997年版，第676 页。

[20]钱大昕：《潜研堂文集·赠谈阶平序》，《嘉定钱大昕全集》第九册，南京：江苏古籍出版社1997年版，第362-363 页。

[21]王记录：《西学究竟在多大程度上影响了乾嘉考据学——以钱大昕为例》，《河南师范大学学报》（哲学社会科学版）2008年第3 期，第152-156 页。

[22]阮元：《畴人传·阮元序》，林文照主编：《中国科学技术典籍通汇·综合卷》第七册，郑州：河南教育出版社1993年版，第137 页。

[23]焦循：《里堂学算记·阮元序》，续修四库全书本。

[24]刘默：《乾嘉学术十论》，北京：三联书店2006年版，第276 页。

[25]梁启超：《中国近三百年学术史》，天津古籍出版社2003年版，第380 页。

[26]阮元：《畴人传·卷四十二·戴震》，林文照主编：《中国科学技术典籍通汇·综合卷》第七册，郑州：河南教育出版社1993年版，第496 页。

[27]田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第141 页。

[28]（美）本杰明·艾尔曼著，复旦大学文史研究院译：《经学·科举·文化史：艾尔曼自选集》，北京：中华书局2004年版，第90、103 页。

[29]焦循：《衡斋算学序》，焦循：《雕菰集》，卷十五，页十五，道光四年（1824年）刻本。

[30]田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第162 页。

[31]焦循：《释弧·自序》，嘉庆四年（1799年）雕菰楼刊本。

[32]焦循：《释轮》，卷上，嘉庆四年（1799年）雕菰楼刊本。

[33]转引自洪万生：《焦循给李锐的一封信》，洪万生主编：《谈天三友》，台北：明文书局1993年版，第144 页。

[34]焦循：《释椭·江藩序》，嘉庆四年（1799年）雕菰楼刊本。

[35]焦循：《上钱辛楣少詹事论七政诸轮书》，《雕菰楼集》，卷十四，页十一。

[36]焦循：《释轮》序，嘉庆四年（1799年）雕菰楼刊本。

[37]焦循：《释轮》序，嘉庆四年（1799年）雕菰楼刊本。

[38]转引自郭世荣：《清代中期数学家焦循与李锐之间的几封信》，李迪主编：《数学史研究文集》第一辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1990年版，第125-126 页。

[39]焦循：《复李尚之言天文推步书》，转引自洪万生：《焦循给李锐的一封信》，载洪万生主编：《谈天三友》，台北：明文书局1993年版，第144 页。

[40]转引自郭世荣：《清代中期数学家焦循与李锐之间的几封信》，李迪主编：《数学史研究文集》第一辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1990年版，第127 页。

[41]中华书局编辑部编：《王韬日记》（增订本），汤志钧、陈正青校订，北京：中华书局2015年版，第259 页。

[42]赵尔巽等：《清史稿·畴人二·华蘅芳》，卷五〇七，列传二百九十四，北京：中华书局1977年版，第46 册，第14015 页。

[43]诸可宝：《畴人传三编·徐有壬》，《中国科学技术典籍通汇·综合卷》第七册，郑州：河南教育出版社1993年版，第657 页。

[44]韩琦：《〈务民义斋算学〉提要》，《中国科学技术典籍通汇·数学卷》第五册，郑州：河南教育出版社1993年版，第647-651 页。

[45]薄树人：《清代对开普勒方程的研究》，薄树人：《薄树人文集》，北京：中国科学技术大学出版社2003年版，第464 页。

[46]这个定理若用综合几何证明常用到椭圆的亚当斯（Adams）性质。如左图，l 为椭圆对应焦点F 的准线，过P 点的切线交l 于K 点。X 为切线PK 上任一点，过X 作XN ⊥l，XM ⊥PF。由椭圆切线性质知道∠KFP 为直角。不难得到XN=e·XM，此即亚当斯性质的结论。如右图，RP，RP′是椭圆的两切线，过R 作RI ⊥l，RN ⊥PF，RM ⊥P′F，由亚当斯性质，知FN=FM=e·RI，不难得到∠PFR=∠P′FR。见（英）A.科克肖特、F.B.沃尔特斯著，蒋生译：《圆锥曲线的几何性质》，上海教育出版社2002年版，第59 页。

[47]陈崧：《椭圆盈缩简法·卷下》，《东溪算学八种》本，宣统二年（1910年），页四，页十二。

[48]中华书局编辑部编：《王韬日记》（增订本），汤志钧、陈正青校订，北京：中华书局2015年版，第250 页。

[49]薄树人先生曾给 （2.3.2）式一个简洁的证明。由椭圆焦点三角形面积公式，又，令两式右边相等，即得（2.3.2）式。（薄树人：《清代对开普勒方程的研究》，《中国天文学史文集》第3 集，北京：科学出版社1984年版）但徐氏是否由此得到该式，也不得而知。

[50]冯立昇、牛亚华：《李善兰对椭圆及其应用问题的研究》，李迪主编：《数学史研究文集》第三辑，呼和浩特：内蒙古大学出版社，台北：九章出版社1992年版，第100-111 页。

[51]田淼：《中国数学的西化历程》，济南：山东教育出版社2005年版，第180 页。

[52]梁启超：《中国近三百年学术史》，天津古籍出版社2003年版，第385 页。

[53]梁启超：《中国近三百年学术史》，天津古籍出版社2003年版，第381-382 页。