徐有壬（1800—1860年），字君青，亦字钧卿，寄籍顺天府（今北京）宛平，原籍浙江乌程（今湖州）人。道光八年（1828年），参加顺天乡试，考取举人。次年，参加会试，中进士，廷试三甲，以主事用，分到户部任职，先后转任户部四川司、山西司、陕西司主事，为官10 多年，由主事升任郎中。之后，历任四川按察使、云南布政使、湖南布政使。咸丰八年（1858年）十二月，任江苏巡抚。咸丰十年四月，太平军攻破苏州城，徐氏殉职，谥号庄愍。徐有壬少时寄居于北京叔父家中，师事钦天监博士陈杰，与沈钦裴、董祐诚、吴嘉善等人有学术交往，后与戴煦、丁取忠、李善兰等人亦有学术来往。徐氏的数学和天文著作经后人整理为《务民义斋算学》出版，共9 种16 卷，其中数学著作7 种12 卷，即《测圆密率》3 卷、《垛积招差》1卷、《椭圆正术》1 卷、《椭圆求周》1 卷、《截球解义》1 卷、《弧三角拾遗》1 卷、《割圆八线缀术》4 卷（吴嘉善述草，左潜补草）。徐氏在当时具有很高的数学地位，王韬曾在日记中记载：

壬叔（指李善兰）谓江南多英俊之士，今君青先生开府吴中，其算学为海内宗师，可于各县书院中别设历算一科，悉心指授，则西学不难大明。^[41]

华蘅芳将徐氏的《弧三角拾遗》与英国海麻士的《三角数理》对比后，“益觉徐有壬《拾遗》三术难能可贵，超越西人”^[42]。诸可宝在《畴人传三编》中论道：“道咸朝吾浙以算学自鸣者夥矣。顾能于古今诸名大家外，因法立法独树一帜者，断推庄愍公焉。”^[43]

张文虎的日记《莲龛寻梦记》（1840年前）中曾记载，他曾手录《务民义斋算学四种》，包括《测圆密率》《椭圆正术》《弧三角拾遗》《表算日食三差》，由此可知，徐氏的《椭圆正术》在1840年前就已成书。^[44]该书与焦循的《释椭》是差不多的研究思路，直接针对《历象考成后编》中椭圆模型所涉及的数学基础，他认为“新法盈缩迟疾皆以椭圆立算，而取径迂回，布算繁重，且皆系借算，非正术也。兹编法归简易，得数较密”。徐氏能以“正术”自称，确有独到之处，他找到椭圆轨道问题的较为“直接”解法。可惜的是，徐氏“于术甚精，而立法之原不以示人”，各术只有术文并无术解。李善兰对《椭圆正术》极为推崇，称其“驾过西人远矣”，“但各术之理俱极精深，恐学者骤难悟”，因此“逐术为补图详解之”写成《椭圆正术解》。此处仅就徐氏“以角求积”术为例，结合李善兰的解证，对徐氏的“正术”作一论述。

如图2-3-1，已知椭圆模型中实行角∠AF1 P=α，要求太阳平均近点角M。

第一步，设焦点三角形中∠AF2P=β，徐氏称之为“借角”，他认为实行角α 和借角β 之间有

由此可得，进而得到在焦点三角形中。

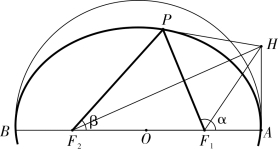
图2-3-1

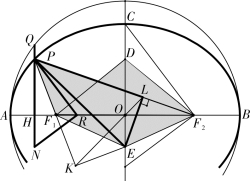
图2-3-2

第二步，借用前一节图2-1-3，∠QOA=E，徐氏给出公式

由此得到E。

第三步，由比例式

得到M=E-esinE，即开普勒方程。

徐氏此术不求向径，较《历象考成后编》中的方法的确更“直接”“简易”，一个重要原因是他运用了式（2.3.1），减省了《历象考成后编》中求较角∠P 的一大段步骤。^[45]但此术的3 个步骤（公式）均非显然可得。

对于式（2.3.1），徐、李二人都没有给出证明。比较直接的解法是运用椭圆的一个几何性质：椭圆的焦点到两切线交点的连线平分焦点对两切线的张角。^[46]如图2-3-1，HP 和HA 为椭圆的两切线，有

由此，（2.3.1）式显然可得，几何意义非常直观。后来曾任潮州金山中学堂教习的陈崧在其《椭圆盈缩简法》（1894年跋）中对徐氏此术进行解读，陈氏就是运用图2-3-1图示解释（2.3.1）式，他说：

太阳行一二象限内，其半对线角与半实引角两割线至圆界外必相合，其相合处必与最卑点之切线相遇，以成公切线（HA）。太阳行三四象限内，其半对线角与实引之半外角两割线至圆界外而合，亦与最卑点之切线相遇，以成公切线。

即两条角平分线的交点必在椭圆过最卑点A 的切线HA 上，因此他称线段HA 为：

两半角之所共，最有用处。其所以能由对线角以求太阳实引角者，皆赖此线，以为枢纽也。^[47]

从几何角度而言，HA 与两条角平分线三线为何共点，徐氏术文中并未说明，李善兰亦未给出证明，陈崧看出了这三线的特殊所在，也没有证明，他们三人均默认应用。按，徐有壬的《椭圆正术》成书年代在1840年以前，椭圆这一性质未见有文献记载，即使是后来的有关圆锥曲线的翻译著作也没有提到这一性质。徐、李二人何以默认（2.3.1）式的正确，其背景有待进一步研究，也许有外来的影响。徐有壬曾有与外国传教士会面的经历，王韬在咸丰九年（1859年）正月十二的日记中记载：(www.daowen.com)

闻徐君青先生升任江苏巡抚。君青先生，浙江乌程人，精于历算。于丁巳（1857年）四月中曾来沪，至墨海观印书车，并见慕维廉、韦廉臣二君，皆以洋酒饼饵相饷，请予为介，得与纵谈。为人诚至谦抑，雍容大度，与壬叔为算学交，最密。^[48]

徐氏精于“历算”，与传教士“纵谈”的内容应该包括算学，不过这之前他有没有接触西方数学目前还没有找到史料支持。

我们认为，在本章第一节图2-1-4中，由梅文鼎的“切线分外角法”，令∠F1F2R+∠R=α，∠F1F2R-∠R=β 代入式（2.1.7）可得式（2.3.1）。

对于式（2.3.2），徐氏也没有证明，李善兰的解证如下。

如图2-3-2，作PR ∥CF2 交AB 于M 点，作RN⊥PR 交PH 的延长线于N 点，得到勾股形RtΔPRN，由，得到PR=QH。由得到c×PN=a×RN。

作PE 平分∠F1PF2 交短轴于E 点，E 作EL⊥PF2，EK⊥PF1 延长线于K点，在短轴上取ED=PN，则有

故

容易得到

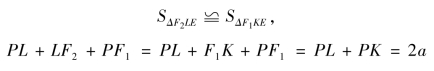
故

PL=a，S四边形PF2EF1=PL×EL=a×EL

故

c×PN=a×EL

又

c×PN=a×RN，故RN=EL。

所以

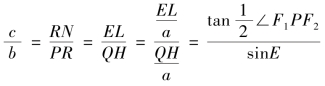
李善兰这个证明具有很强的构造性，他相当于在大辅圆中构造了半较角∠P 对应的正切线段EL 和偏近点角对应的正弦线段QH，在两条共点焦半径（PF1，PF2）截取了等于半长轴的线段PL。^[49]

对于（2.3.3）式，李善兰给出的解证如下。

借用前一节图2-1-3，有

ΔODF1 与ΔOQF1 为同底三角形，则

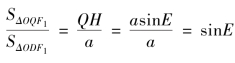
其中，不难得到式（2.3.3）。