焦循（1763—1820年），字理堂，号里堂，江苏甘泉（今扬州）人。嘉庆六年（1801年）举人。次年，赴京会试不第，自此决意居家，远离城市，潜心著述。焦循博闻强识，识见精卓，经、史、历算、音韵、训诂无所不通，尤擅易学。所著书多达数百卷，身后被称之为“通儒”。焦循曾自称：

予幼好九九之学，虽求之古书而不能得其指归。自交吴中李尚之锐、歙县汪孝婴莱，得两君切磋之益，于此艺少有进。而两君亦时时以所见示，令商论其可否。^[29]

因此，焦循、李锐、汪莱三人有“谈天三友”之誉。1787年，顾凤毛（1762—1788年）赠送焦氏一部《梅氏丛书辑要》，从此焦氏开始学习和研究数学，并撰写数学著作，时间主要集中在1794—1801年间。这个时间又可分成两个阶段。^[30]第一阶段是1794—1796年间，他的主要工作集中在平面三角和弧三角学的阐释方面，撰成《释弧》三卷（1795年秋草成）、《释轮》二卷（1796年二月序成）、《释椭》一卷（1796年九月序成）。《释弧》草成于1795年秋，原分三篇，“上篇释正弧弦切之用，中篇释内外垂弧之义，下篇释次形及矢较之术”。三年后，又觉得所论“立表之理不明，由裁弧为弦之法不备，宜补之”。故将昔年所论的“六弧八线”补为上卷，上中两篇合为中卷，下篇不动仍为下卷，共三卷。^[31]该书主要是在梅文鼎的《弧三角举要》《环中黍尺》以及戴震的《勾股割圜记》的基础上，讨论球面三角形的解法。《释轮》分析了传入的第谷天文体系中均轮、次轮的几何原理，“上篇言诸轮之异同，下编言弧线之变化，以明立法之意”^[32]。《释椭》讨论了传入中国的卡西尼天文学说中的椭圆知识。焦氏的这三部著作主要目的是总结当时天文学中的数学知识基础。焦氏曾在给李锐的信中谈及这些著作的写作原由，他称：“因学椭圆，即为《释椭》，因学弧三角，即为《释弧》。因学交食及五星诸轮法，即为《释轮》《释交》。”^[33]

第二阶段是1799—1801年间，焦循主要撰写了对复显于世的数学著作的研究心得，有《加减乘除释》八卷（1799年）、《天元一释》（1800年）、《开方通释》一卷（1801年）。此后，他潜心研究《易》学和《孟子》，数学方面的成就仅于1814年著成《大衍求一术释》。

江藩在给《释椭》作序时称：

嘉庆三年（1798年）秋，里堂出所制《释椭》一篇示予。考西法：自多禄亩（即托勒密）以至第谷，皆以日月五星之本天为平圆；其后西人有刻白尔（即开普勒）、噶西尼等以为椭圆，两端径长，两腰径短。雍正八年六月朔日食，旧法推得九分二十二秒，今法推得八分十秒。验诸，诏用今法。椭圆起于不同心，天之两心差引而倍之，为倍心差；用面积求平行实行之差，于是有大小径中率与平圆之比例及差角之加减度，与旧法不同矣。其法以面积之度与角度相较，亦可得平行实行之差。然平行，面积也；实行，角度也。以积求角难，以角求积易。故先设以角求积，次设以积求角，次设借积求积，次设借角求角。四法最为简捷，与旧法迥殊。其言日躔之理亦即盈缩高卑之说也。……是篇仿张渊观象赋之例，自为图注，反复参稽抉蕴阐奥，为实测推步之学者所不可无之书也。学者从事于斯，以求日躔月离交食诸轮，无晦不明，无隐不显矣。^[34]

《释椭》全文实际上是从数学角度解释《历象考成后编》中椭圆模型所涉及的数学知识，属于“历算”范围。焦循自序也称：

康熙甲子律书用诸轮法，雍正癸卯律书用椭圆法。盖实测随时而差，则立法亦随时而改。循习此术，以义蕴深密，未易寻究，谨择其精要析而明之，庶几便于初学云尔。

焦氏是按“定义—性质（公式）—定理（预备算法）—椭圆算法推导”的顺序来解释“椭圆之法”。

定义包括椭圆以及椭圆各种基本量：地心差（焦半径）、大小径（长短轴）、中半径（长短半轴积的根，即）、径线（向径，焦半径）、心差角（从椭圆中心出发的两条半径的夹角，对应“平行角”）、地心角（同一焦点的两条向径的夹角，对应“实行角”）、椭圆之积（向径扫过的面积）、椭圆差角（椭圆上一点对应的椭圆中心角与大辅圆中心角之间的椭圆扇形）。

性质（公式）：

（1）椭圆上一点到两焦点的距离和等于长轴，即所谓“以两腰线，凭椭弧而施之，同其底，则两腰之度较异而和同”，由此性质可以画椭圆。

（2）椭圆面积公式，将椭圆看成半径为中半径的圆，即S椭=πab。

（3）椭圆面积定理，即“椭圆以地心为心，分其度为三百六十，抵最卑则短，抵最高则长，每度不均于弧而均于积也”。

定理（预备算法）：

（1）椭圆基本定理。焦氏认为这个性质很重要，是沟通椭圆和辅圆关系的“枢纽”，称“大小径者，比例之根也”；“大小径比例之法，至精至妙”。

（2）椭圆焦半径的3 种算法。焦氏总结出《历象考成后编》涉及焦半径长度的3 种算法，在焦点三角形ΔF1PF2 中，称∠AF1P 为外角，∠P 为“均数”（参考图2-2-1）。

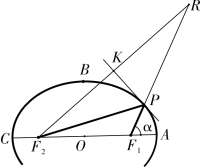
图2-2-1　求向径法一

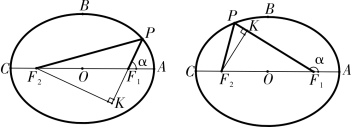
图2-2-2　外垂线法和内垂线法

法一，如图2-2-1，延长F1P 至R 点，使得PR=PF2，在三角形ΔF1RF2 中，F1R=F1P+F2P=2a，先求出∠R 及F2R，进而得到PR，即焦半径PF2。此法中R 点很重要，焦氏称F1R“两腰之和，求角之要”。

法二和法三，如图2-2-2，过F2 作F2K ⊥F1P，因为垂线F2K 在焦点三角形形外和形内，焦氏称之为“外垂线法”和“内垂线法”，即所谓“内垂外垂，两腰之用也”。

椭圆算法的推导：

椭圆“角”“积”互求的4 种算法，即以角求积（“有地心之角度可以求椭圆之面积”）、以积求角（“有椭圆之面积可以求地心之角度”）、借积求积（“有心差之角度可以得椭圆之面积”）、借角求角（“有心差之角度可以求地心之角度”）。

以“借积求积”为例说明焦氏的推理特点，如图2-2-3，过程如下。为节省篇幅，参照前一节的推算说明，此处推理过程不作详细解释，括号里为简单的随文注释。

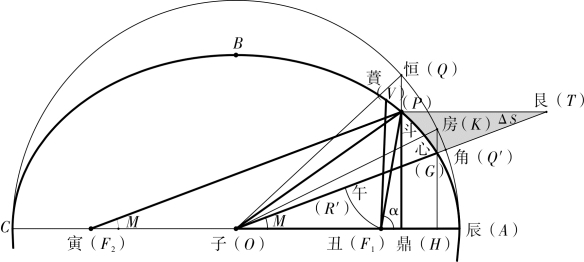
图2-2-3　焦循释“借积求积”

有子角角辰度（∠AOQ′，记为M）求丑斗辰面积（S向径扫过积F1PA）。先以角辰度为寅角（∠AF2P），用内垂线求得丑斗（F1P）。以丑斗为半径求得斗鼎（PH），用大小径比例求得鼎恒（QH）以为正弦检表的恒辰弧度（∠AOQ），……得子恒辰面积（S扇形AOQ）。又用大小径比例得子斗辰面积（S椭扇AOP）。存之。

用大小径比例得房辰（∠AOK），……得子房辰面积（S扇形AOK）。用大小径比例求得子心辰（S椭扇AOG）。乃以子心辰减所存之子斗辰，余子斗心积数（S椭扇POG=S椭扇AOP-S椭扇AOG）。存之。(www.daowen.com)

用心差子丑乘斗鼎折半得子斗艮（SΔOPT），减子斗心，余斗心艮一钝二锐形（S弧三角形GPT=SΔOPT-S椭扇POG，记为ΔS）。此形与子丑午同，知此即知子丑午面积矣（S弧三角形OF1R′=ΔS）。

既得子丑午面积，即得丑斗蕡积数（S椭扇POV=ΔS）。用以积求角法求得斗蕡度（∠PF1V=Δα），加斗辰得辰蕡实行度（α=Δα+∠AF1P）。

此处“借积求积”是《历象考成后编》中“借积求积”术的第二种，前一节叙述（图2-1-5）的是第一种，区别在于直接作F2P 平行于OQ′，∠AF1P=M+∠P。在说理过程中，焦氏没有具体的计算，呈现的是一种演绎推理的风格。

在焦循所处的时代，中国存在中西两种历算体系，同时也恰逢宋元数学复兴，焦氏曾在《复李尚之言天文推步书》中称：

推步之学，自三统历十三家，至元郭守敬作授时术，明大统依之，徐氏辑新法历书，西法渐备，于是弟谷、穆尼阁、噶西尼之徒，各运其巧思，积久而密。

这种状况造成了混乱，就是西方历法也有“不同心圆”“诸轮法”与“椭圆法”之别，这些使得“后之学者，或执中以辟西，或用西而谤中，或援西于中，或以中证西，互执其理，丛樌不一”，以至于有人认为“天文度数有定，似难而实易”。加之汉唐宋元算书的复显，数学知识量的突增。如何从算理上对历算（“推步之学”）和数算（“测算之学”）进行统一是当时面临的一个问题。

1796年初，完成《释轮》初稿后，焦循上书曾给《释弧》作序的钱大昕，一则表示感谢，二则就学习本轮—均轮模型的心得求教于钱氏，他说：

窃思弟谷以来，诸轮之设或左行、或右行、或倍行、或三倍行、或自远、或自近、或自平远、或以本轮为心，大率皆以实测所得之数假为法象，以曲求其合，故不能比而同之也。^[35]

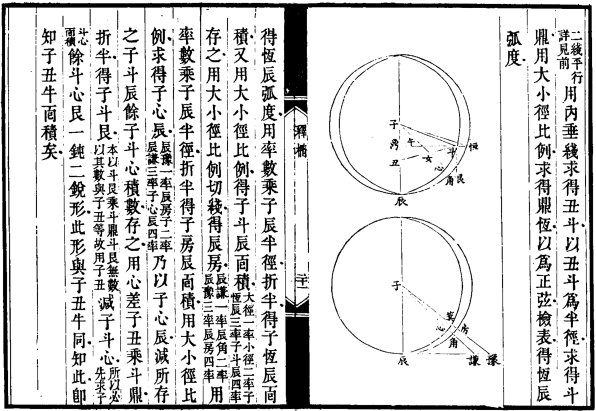
焦循《释椭》“借积求积”（续修四库全书本）

钱氏非常赞同焦氏关于本轮—均轮模型“以实测所得之数假为法象”的观点，称赞《释轮》“所论月五星诸轮推阐入微，以实测之数假立法象，以求其合，尤为洞澈根原”^[36]。并向焦循推荐了自己的高足李锐。之后，李锐对焦循的研究心得也有一番议论，于嘉庆元年（1796年）二月写信对焦循说：

足下又云“有其当然，亦必有所以然”。锐愚以为，其所以然不外乎所当然也。何者？古法有三统以来，见存者约四十家，其于日月之盈缩迟疾、五星之顺留伏逆，皆言其当然而不言其所以然。本朝时宪书甲子元用诸轮法，癸卯元用椭圆法，以及穆尼阁新西法用不同心天，蒋友仁所说地动仪，设太阳不动而地球如七曜之流转，此言其当然，而又设言其所以然。然其当然者，悉凭实测；其所以然，止就一家之说。衍而极之，以明算理而已。^[37]

我们知道，中国古代历法优劣是以是否符合观测现象为依据，“悉凭实测”是制定历法的基础，“历之本在于验天”，对天体运动轨迹的几何模型不甚关心，确实“皆言其当然而不言其所以然”。而欧洲天文学是以一套完整的、量化的、系统化的几何模型为基础，明末清初传入的系列几何模型就是它们认为日月五星的“所以然”。但是传统历法“不言其所以然”，西方诸法“其当然者，悉凭实测；其所以然，止就一家之说”。李锐认为焦循探寻“所以然不外乎所当然”，而他谋求的是将西方诸法统一到“算理”上来。基于这样的认识，李锐提出了中西历法“愈改愈密”的观点，并对焦循说出了自己的“三大愿”：

辛亥（1791年）冬间，从竹汀师（指钱大昕）游，受推步算术之学，迄今五六年，稍能窥见藩篱，而后知此道之精微广大，有毕世为之不能尽者，是故有大愿焉，请为足下陈之。

中法自《三统》以至《授时》《大统》，载在廿四史者甚备，然史学家自吾师考异而外罕言及者。意欲随术讨论，于法之隐奥者详说之，字之误者正之，文之脱者补之，不可考者阙之，俾古人创造之法、愈改愈密之苦心不致泯没无传，则所愿一也。

本朝时宪书用西方本轮、次轮，以及椭圆面积之术，至精密矣。溯其所自来，唐有《九执》，元明有《回回》二家，国初又有未经行用之穆尼阁《天步真原》。是三术者，《九执》则传写脱误处甚多，《回回》则月分最高之元术中并未明载，穆尼阁、薛仪甫所译，言之不详。亦思有以剖析之，使谈西学者知彼中测验亦由疏而密，非一蹴可到，则所愿又一也。

唐宋相传有算学十书，今《缀术》亡矣，存有九种。《周髀》为盖天遗说，《九章》于算数之事纲举目张，《海岛》用矩表测望高深广远，《缉古》开从立方，为后来立天元一、借根方之所自出，孝通自云，如有排其一字，臣欲谢以千金，则其立术之精深可知矣。亦欲一一究明其所以然，无所疑惑而后快，则所愿又一也。^[38]

李锐的第一愿就是要全面研究中传统天文历法，对古代各家历法进行综合分析、补缺正误、阐微发隐，“俾古人创造之法、愈改愈密之苦心不致泯没无传”；第二愿是要剖析传入的西方历法，“使谈西学者知彼中测验亦由疏而密，非一蹴可到”；第三愿就是解释中国古代数学，“亦欲一一究明其所以然，无所疑惑而后快”。总的来说，李锐三大愿实际上就是想要对中西历算和中西数算的“所以然”进行阐释。

同样的，我们看到焦循的系列“释作”其实也是冲着阐释“所以然”这个目的去的，他说：

自己酉（1789年）以来，方读梅氏《少广拾遗》，即为《乘方释例》五卷；因学椭圆，即为《释椭》；因学弧三角，即为《释弧》；因学交食及五星诸轮法，即为《释轮》《释交》，其杂述类聚之文又二三十篇。皆就已之所已明者言之尔。

更进一步，焦循也在考虑“九章等术所以然之故”，他说：

九章等术所以然之故，前人颇言之，而未能了然。循尝以推算之妙，其转移变换，惟在加减乘除；自“九章”距测，以及弧三角、矢较、椭圆诸法，皆不外四者之用。鄙意欲通为一编，以四者为经，而运会其所有用之故，庶可驭繁于简，言归于要。^[39]

这个“所以然之故”就是焦循后来的《加减乘除释》。他以加减乘除四种运算为纲，将算学之“所以然”归于“加减乘除”，而将“推步之学”归于“四者之用”。这样“历算”和“数算”统一于“加减乘除”。所以他听说李锐的“三大愿”后，就其“加减乘除释”的观点写信问李锐：“可与兄之愿相为表里否？”李锐在后来的回信中没有回答这个问题，但提出了自己对历算“所以然”的认识思路，他说：

借根方西人名为东来法，梅总宪（指梅瑴成）谓即古立天元一是也。锐尝推而论之，元郭守敬求周天矢度，用开带从三乘方，立天元一法也。西人求每弧通弦，用诸等边割圆，借根方法也。借根方即立天元一，则有天元一而后有借根方，有借根方而后有八线表，有八线表而后有弧三角法，有弧三角法后测验密，测验密而后推步精。^[40]

这是一个明晰的递归的解释进路：立天元一→借根方→八线表→弧三角→测算之学→推步之学。在这个进路中，李锐坚定而又明确地将当时中西“推步之学”和“测算之学”递归统一到中国古代数算中的“立天元一”上。当然，这中间有“西学中源”思潮的影响，但传统数学的复显给了当时中国数学家以知识储备和化归、解读西学的自信。（本书将在结语部分对此进行进一步论述）

如果“创造之法愈改愈密”，那么《历象考成后编》的“椭圆之法”就是“推步之学”的最高级了。为了消除中西之法“互执其理，丛樌不一”，焦氏“择其精要析而明之，庶几便于初学”写成的《释椭》，就是对历算进行数理解释，只不过焦氏后来把它们归于“加减乘除”了。

《历象考成后编》中所有的运算均用具体的算例为范例，并没有给出公式性的结论，焦循的《释椭》实际上将椭圆模型涉及的数学基础系统化、理论化，并且补充了数学证明。焦氏关注天文问题的数学基础，解决和系统化了《历象考成后编》所涉及的数学基础。他的这种阐释方式影响到后来的学者，很多学者将目光关注到算法的改进和阐释上，有的直接把它们当成数学问题进行研究。之后的徐有壬和李善兰的研究可谓代表。

乾嘉学派的学风导致儒家学者关注天文历法以及相应的数学基础，当时复兴的宋元数学给予他们“会通”西学的自信和中算基础，数学说理崇尚一般化，数学研究的社会地位提高，成为“专家之学”，研究也趋向了专业化或专门化。