《后编》虽然采用了颠倒的椭圆定律和面积定律，但从数学推算的角度来看，倒没有什么区别。这两方面实际上就是椭圆向径扫过面积、椭圆扇形面积及其大辅圆扇形面积相互转化的问题。关于《后编》对椭圆轨道问题的几何推算，李俨先生首次对该问题进行论述^[10]，薄树人的《清代对开普勒方程的研究》从天文学的角度指出该问题实际上就是开普勒方程的推导^[11]，牛亚华的《明末清初椭圆知识的传入及应用》则从数学角度对该问题进行了论述^[12]。本节结合前人的研究，以“以角求积”术为例探讨《后编》对该问题的探讨，以体现其方法特点。要指出的是，《后编》是用具体的计算实例来介绍算理的，在此改用一般的叙述方法。

如图2-1-3，设椭圆ABC 为太阳的椭圆轨道，O 为中心，长半轴OA=a，短半轴为OB=b，偏心率为e，两个焦点为F1 （地心）和F2。太阳在P 点，相对于地心F1 作“匀面积”运动，《后编》称“太阳循椭圆周行，惟所当之面积相等，而角不等”。∠AF1P=α 为已知，《后编》称之为“实行”，即现今所谓的真近点角。现在椭圆上找一点P′，使得椭圆扇形面积AOP′与椭圆向径扫过面积AF1P 相等 （《后编》称后者为“实行积”），即S椭扇AOP′=S实行积AF1P，但这两个面积都不易推算。于是过P′作P′Q′⊥OA，交OA 于点T′，交大辅助圆于点Q′；再过P 作PT ⊥OA，交OA 于点T，交大辅助圆于点Q。这样分别得到椭圆扇形面积AOP′和向径扫过面积AF1P 在大辅圆中对应的面积AOQ′和面积AF1Q，两对对应面积可由椭圆基本定理建立联系。《后编》称∠AOQ′为“平行”，现今天文学称为平近点角，一般记为M；∠AOQ 即现今的偏近点角，一般记为E。

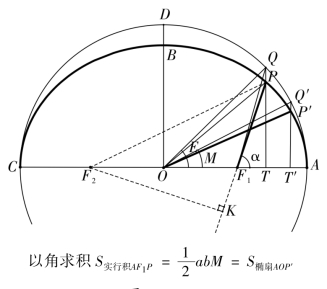
图2-1-3

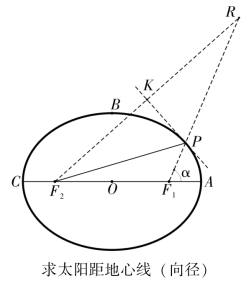
图2-1-4

已知真近点角α，求椭圆向径扫过面积AF1P 的算法，《后编》称之为“以角求积”。算法过程简介如下：

在图2-1-3中，延长PF1至K，作F2K ⊥PK，则在直角三角形F2KP 中，

所以椭圆向径F1P（《后编》称之为“太阳距地心线”）为

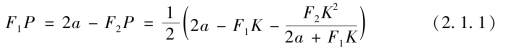
由椭圆基本定理有，而PT=PF1sinα，所以

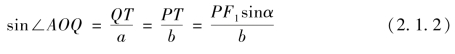
由此可得∠AOQ，记为E。

又

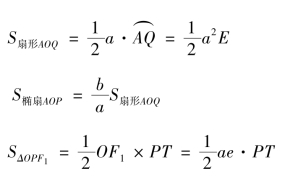
所以实行面积为

又由椭圆基本定理可得，而

又

所以实行面积可以表示为

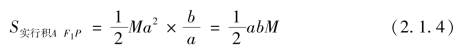
由式（2.1.3）和式（2.1.4）可得平行角M。

实际上，由式（2.1.1）可以得到

再由式（2.1.3）和式（2.1.5）可得

即

这就是著名的开普勒方程。

《历象考成后编》卷一“以积求角”第一页（光绪丙申励志书屋刊本）

在椭圆轨道理论中，行星的近点运动规律是用开普勒第二定律描述，行星运动是绕焦点作“均面积”运动，近点角用椭圆向径扫过面积来度量。而真近点角a 与平近点角M 之间的关系则要通过一个中间变量（偏近点角E）来联系，而后两个量的关系由开普勒方程确定。

从数学角度而言，“以角求积”实际上是已知椭圆轨道长半轴a，偏心率e 和实行角α，通过式（2.1.1）或式（2.1.5）得到向径，再由式（2.1.2）得到偏近点角E，最后由开普勒方程得到平近点角M。本质上是要把椭圆中张角为α 的向径扫过面积转化成大辅圆的扇形面积，并求出相应的圆心角M。

《后编》“椭圆角度与面积相求”中还介绍了另一种方法求向径PF1，即式（2.1.1）。如图2-1-4，延长F1P 至R 点，使得PR=PF2，连接RF2，用“切线分外角法”求得∠R。过P 点作PK ⊥RF2，在ΔF1RF2 中运用正弦定理得到F2R，由RK=F2R=PRsin∠R 以及F1P=2a-PR 得到F1P。(www.daowen.com)

所谓的“切线分外角”法，《后编》并没有给出详细的解说，我们认为此法应该来自梅文鼎的《平三角举要》。此书卷二“又术（用切线分外角）”以及卷四“或问”中的“用切线分外角之理”讲解了已知三角形的两边及其夹角，直接求另外两角的一种几何方法。在ΔABC 中，已知两边a，b 及夹角C，求另外一角B。梅文鼎称运用正弦定理不能直接得到B，而运用三角公式（a+b）：（a-b）=tan：tan以及可直接得到B，其中A+B=π-C 为C 的外角。在证明过程中，梅氏将已知三角形置于圆中，运用了圆的切线性质，并图示出了公式中各量所对应的半角和线段。梅氏称此法为“用切线分外角”。^[13]

仿此，求∠R 的具体步骤应为，在ΔF1RF2 中，由

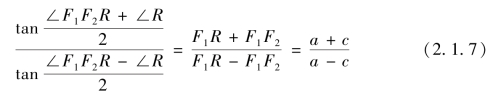
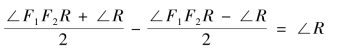
得到∠R。

可以看出，《后编》利用纯粹的几何方法探求E 与M 之间的关系，其主要的数学知识基础是几何图形面积的计算、平面三角知识、椭圆基本定理和椭圆切线的性质。

反过来，由平近点角（平行）求真近点角（实行），《后编》给出了三种方法：“以积求角”“借积求积”和“借角求角”。这三种方法《后编》用的都是几何方法，均为近似算法。如“以积求角”是从近地点开始，对平近点角M 逐度依次求出太阳相应的真近点角αi 后的和Σαi（=α）即为对应的实行角。由面积定律，设对于平行角椭圆逐度面积为S0，太阳的位置依次为P1（=A），P2，P3，…，则，∠PiF1Pi+1=αi，i=1，2，3，…。《后编》认为椭圆面积PiF1Pi+1 近似为一个扇形，它的半径为F1Pi，张角为αi。第一个1°时，F1P1=a-c，容易得α1。第2 个1°时，由“以角求积”术中向径的算法可以得到F1P2，进而得到α2。如此逐度计算，得到α3，α4，α5，…，最后将它们相加得到α=Σαi。显然这是近似计算。

“借积求积”术。已知平近点角∠AOQ′=M，求真近点角。如图2-1-5，找到Q′点在椭圆的对应点P′，过点F2 作F2V ∥OP′ 交椭圆于V 点，则∠AF2V=∠AOP′，记为M′。《后编》认为太阳应在V 点附近的P 点，真近点角∠AOP=α 为所求，它与∠AF1V 有一个差角∠PF1V，记为Δα。

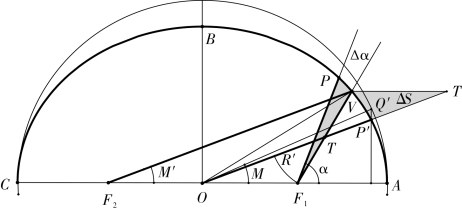
图2-1-5　借积求积

根据“以积求角”术中算法可以求出∠AOP′，面积S椭扇AOP′。运用切线分外角法得到∠F2PF1，则∠AF1V=M′+∠F2VF1，面积S向径扫过积AF1V 可求。

设F1V 与OP′交于T 点，弧三角形F1TR′与弧三角形VTP′关于T 点中心对称，则面积S椭扇AOP′ 与面积S向径扫过积AF1V 相差一个面积S弧三角形OF1R′，即

这个面积差记为ΔS。因为S向径扫过积AF1P=S椭扇AOP′，所以

《后编》认为，S向径扫过积VF1 P=S弧三角形OF1R′，即等于ΔS，则有

所以

α=∠AF1V ± Δα（符号与M 值有关，图示情形为象限前，用“+”。）

Δα 由ΔS 导出，方法如下。

利用“以角求积”术中向径求法得到向径F1V。过V 点作VT ∥OA 与OP′交于点T，则

∠AOV，∠AOP′可求，借助椭圆基本定理可以导出上式中最后3 个面积，则面积差值ΔS 可求。《后编》认为，面积S向径扫过积PF1V（ΔS）既然已知，则可以运用“以积求角”术得到Δα，即把这块面积看成半径为F1V，张角为Δα，面积为ΔS 的圆扇形。可以看出，此术“所借之积”指的是ΔS。

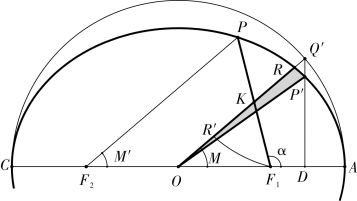
图2-1-6　借角求角

“借角求角”术。此术是已知平近点角∠AOQ′=M，求真近点角的另一种近似方法。如图2-1-6，找点P′为Q′点在椭圆的对应点，OQ′交椭圆于R 点，过点F2 作F2P ∥OQ′交椭圆于P 点，《后编》认为此时椭圆扇形面积S椭扇AOP′ 等于向径扫过面积S向径扫过积AF1P，即S椭扇AOP′=S向径扫过积AF1P，则∠AF1P 就是所求的近点角α。算法原理简介如下：

在焦点三角形ΔF1PF2 中运用切线分外角法得到∠P，由椭圆基本定理可以由∠AOQ′得到∠AOP′，则∠AF1P=∠P+∠AOP′=α 即得。

至于S椭扇AOP′=S向径扫过积AF1P 为什么成立？如图示，设OR 与F1P 交于K 点，弧F1R′与弧PR 关于点K 中心对称，则

《后编》认为

故

从计算步骤来看，这个算法是后三法中最简单的，但是也是误差最大的，误差来源于式（2.1.7）。

实际上，在给定平近点角的情况下，要通过解开普勒方程才能够求得真近点角。而开普勒方程是一个超越方程，无法精确求解，只能近似求解。开普勒之后，接受椭圆假说的许多欧洲天文学家都致力于从几何上构建开普勒第二定律的等效形式，即开普勒方程的几何解法。石云里研究认为，《后编》平近点角和真近点角互求的方法实际上是英国天文学家薄利奥（Ismael Boulliau，1605—1694年）方法的简化版，所用模型来源于薄利奥的模型，只不过传教士把它们归功于卡西尼。正是因为《后编》引进了开普勒理论，其日行理论总体精度较之《历象考成》提高了10 倍以上，为清代后来的交食预报精度的提高奠定了直接的基础。^[14]

从数学上讲，《后编》给清代士人引介了椭圆模型以及相关的算法，这些决定了在新的内容传入之前清代早期学者对圆锥曲线（椭圆）知识研究的内容和限度。