1.行星运动的椭圆定律和椭圆作法

《后编》^[9]卷一“日躔数理”中“用椭圆面积为平行”一节介绍说：

太阳之行有盈缩，由于本天有高卑。春分至秋分行最高半周，故行缩而历日多。秋分至春分行最卑半周，故行盈而历日少。其说一为不同心天，二为本轮。而不同心天之两心差，即本轮之半径，故二者名虽异而理则同也。第谷用本轮以推盈缩差，惟中距与实测合，最高前后则失之小，最卑前后则失之大。又最高之高于本天半径，最卑之卑于本天半径者，非两心差之全数，而止及其半。故又用均轮以消息乎其间，而后高卑之数，盈缩之行，与当时实测相合，《上编》言之详矣。然天行不能无差，……乃设本天为椭圆，均分椭圆面积为逐日平行之度。则高卑之理既与旧说无异，而高卑前后盈缩之行乃俱与今测相符。

此段相当于给出行星运动的椭圆定律。如图2-1-1，太阳P （椭圆上任一点）绕着为地心F1的轨道为椭圆ABCD，其中a 为长半轴，b 为短半轴，c为两心差（焦心距），α 为实行度（真近点角），面积AF1P 为实行积，E 为偏近点角，r 为太阳距地心线（椭圆向径），QH 为平圆正弦，相应的PH 为椭圆正弦。

《后编》中给出了椭圆的两种作法。第一种作法，如图2-1-1：

以甲巳（F1，F2）两点各为心，午（B）为界，各用一针钉之，围以丝线，末以铅笔代午针引而旋转，即成丑午巳未（ABCD）椭圆形。

此即运用了椭圆第一定义（到两定点的距离和等于定长的点的轨迹）作图，现在一般形象称之为拉线法。

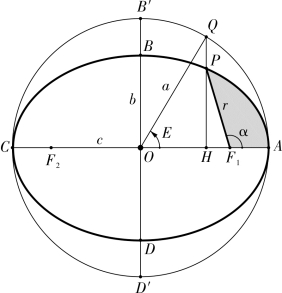
图2-1-1

图2-1-2

在“椭圆角度与面积相求”一节介绍了椭圆的另一种作法：

以甲（F1）为心，以二千万（2a）为半径作圆[ ⊙F1（2a）]。又取两心差之倍度（2c）截直径于丙（F2），自丙出线至圆周（F2 R），折半作垂线（HP），所抵圆径之点（P）即椭圆界。依法逐度作点（Pk）连之，即成椭圆周。

如图2-1-2所示，以点F1 为圆心，以2a 为半径作圆，在一条半径上取一点F2，使得F1F2=2c，在圆上任取一点Rk，作F2Rk 的中垂线HkPk 交F1Rk于点Pk，依次连接Pk，即可得到椭圆。这个作法中，F1Rk+F2Rk=2a，相当于还是运用了椭圆的第一定义，可以证明，直线HkPk 其实是椭圆过Pk 点的切线，故《后编》称“以此发明椭圆之理，最为精巧”。

2.行星运动的面积定律(www.daowen.com)

《后编》卷一“日躔数理”中“用椭圆面积为平行”一节介绍说：

乃设本天为椭圆，均分椭圆面积为逐日平行之度，则高卑之理，既与旧说无异，而高卑前后盈缩之行，乃俱与今测相符。

太阳在椭圆周右旋，其所行之分椭圆面积日日皆相等。

此即开普勒行星运动第二定律——面积定律：在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的。只不过这是颠倒的面积定律，以地为中心，太阳绕着地球旋转。

3.椭圆基本定理和椭圆面积算法及其证明

《后编》卷一“日躔数理”中“求两心差及椭圆平圆之比例”一节介绍说：

平圆正弦（QH）与椭圆正弦之（PH）比例必同于平圆半径与椭圆小半径比例也。

平圆面积与椭圆面积之比例，同于平圆外切正方面积与椭圆外切长方面积之比例，亦即同于椭圆大径与小径之比例。……平圆、椭圆二面积依壬癸（B′D′）横径缕析之，则皆成线矣。其线与线之比既同于大径与小径之比，则面与面之比亦同于大径与小径之比。

第一段话介绍的即为椭圆基本定理，如图2-1-1，PH：QH=大径：小径=b：a。第二段话相当于用卡瓦列里原理说明了椭圆与其大辅圆的面积关系是S椭：S圆=大径：小径=b：a，即椭圆面积为S椭=πab。

4.平行与实行互求

《后编》卷一“日躔数理”中“椭圆角度与面积相求”一节介绍说：

《前编》言，以面积之度与角度相较，而平行实行之差以出。盖太阳距最卑后平行之度，必与太阳距地心线所分之面积等，故可以平行度为面积而求实行也。然实行固角度也。以实测言之，则先得实行，后求平行。以角而求积也，易。以推步言之，则先设平行，后求实行。以积而求角也，难。故先设以角求积之法，可以知数理之实；次设以积求角之法，可以知比例之术；次设借积求积、借角求角之法，可以知巧合补凑之方。反复参稽，而数之离合乃纤悉毕呈焉。

设太阳轨道的长半轴、偏心率为已知，则关于太阳运动的计算有两个方面。一方面是从实际观测到的太阳离开轨道近地点的距离，即现今的真近点角，《后编》称为“实行”，算出太阳椭圆轨道向径扫过的椭圆面积，由此算出按平均运动计算的所谓平均近点角，《后编》称为之“平行”。另一方面则是通过平均运动推求在给定时刻的太阳的观测位置。前者称之为“以角求积”；后者《后编》给出三种解法，分别叫做“以积求角”“借积求积”和“借角求角”。这几种算法的精度决定了天文现象预测的精确度，是后世历算关注的焦点，介绍如下。